Ceci est une ancienne révision du document !
ETSN 2022 : les GPU, la technologie disruptive du 21ème siècle
Cette session de travaux pratiques se compose de 7 séances de 1h30 du workshop Les GPU, technologie disruptive du 21ème siècle. Elle s'accompagne de 5 cours donnés par Emmanuel Quémener.
CQQCOQP : Comment ? Qui ? Quand ? Combien ? Où ? Quoi ? Pourquoi ?
- Pourquoi ? Faire un tour d'horizon des GPUs et appréhender des méthodes d'investigation
- Quoi ? Programmer, tester et comparer les GPU sur des exemples simples pendant 6 séances de 1h30 heure
- Quand ? Entre le 25 et le 29 juillet 2022
- Combien ? Mesurer la performance que les GPUs offrent en comparaison des autres machines
- Où ? Sur des stations de travail, des noeuds de cluster, des portables (bien configurés), dans des terminaux
- Qui ? Pour les édudiants, enseignants, chercheurs, personnels techniques curieux
- Comment ? En appliquant quelques commandes simples, généralement dans des terminaux.
But de la session
C'est de prendre en main les GPU dans les machines, d'appréhender la programmation en OpenCL et CUDA, de comparer les performances avec des CPU classiques par l'intermédiaire de quelques exemples simples et des codes de production.
Déroulement des sessions pratiques
Le programme est volontairement touffu mais les explications données et les corrigés devraient permettre de poursuivre l'apprentissage par la pratique hors de cette école d'une unique semaine.
- Prise en main de l’environnement à distance du Centre Blaise Pascal à l'ENS-Lyon
- Découverte du matériel, autant CPU que GPU
- Exploration progressive en OpenCL avec l'exemple de base de la documentation Python/OpenCL
- Un intermède Python/CUDA pour tester l'autre implémentation sur GPU
- La réalisation et le portage d'une transformée de Fourier discrète
- Choix du périphérique en Python, sa programmation
- Utilisation des librairies externes, exemple avec xGEMM
- Expoitation de codes Matrices pour la métrologie
De manière à disposer d'une trace de votre travail et de pouvoir l'évaluer, il est recommandé de rédiger un “livre de bord” sur la base des questions posées. N'hésitez pas à faire des copies d'écran et à les intégrer dans votre document.
Démarrage de la session
Prérequis en matériel, logiciel et humain
De manière à proposer un environnement pleinement fonctionnel, le Centre Blaise Pascal fournit le matériel, les logiciels et un OS correctement intégré. Les personnes qui veulent réaliser cette session sur leur laptop doivent disposer d'un “vrai” système d'exploitation de type Unix, équipé de tout l'environnement adéquat.
Prérequis pour le matériel
- Si vous n'utilisez PAS le CBP, une machine relativement récente avec une GPU intégrée avec circuit Nvidia
- Si vous utilisez le CBP, un laptop disposant d'un écran assez confortable pour afficher une fenêtre de 1024×768, une connexion réseau la plus stable possible et la capacité d'y installer un logiciel adapté.
Prérequis pour le logiciel
- Si vous n'utilisez pas le CBP, un OS GNU/Linux correctement configuré pour la GPU embarquée avec tous les composants Nvidia, OpenCL, PyOpenCL, PyCUDA. A cela s'ajoute un navigateur pour voir cette page ainsi qu'un traitement de texte pour rédiger le compte-rendu de ces séances.
- Si vous utilisez le CBP, il faut avoir installé le logiciel x2goclient suivant les recommandations de la documentation du CBP. Il est recommandé d'exploiter le traitement de texte et le navigateur dans la session distante.
Pour choisir “judicieusement” une machine parmi les plus de 130 de machines à disposition, consultez la page Cloud@CBP. Il est recommandé de prendre une machine disposant d'une GPU de type “Gamer” ou d'une “GPGPU”. Les sélecteurs de la page précédente peuvent vous aider dans ce choix. Coordonnez-vous entre vous pour être si possible chacun sur la vôtre. Ensuite, une fois connecté via x2go, il peut être intéressant de se connecter sur une autre machine de configuration différente pour comparer les résultats de vos expérimentations.
Prérequis pour l'humain
- Une allergie à la commande en ligne peut dramatiquement réduire la portée de cette session pratique
- Une pratique des scripts shell sera un avantage, sinon vous avez cette session pour parfaire vos connaissances.
Investiguer le matériel GPU
Qu'y a-t-il dans ma machine ?
Le matériel en Informatique Scientifique est défini par l'architecture de Von Neumann:
- CPU (Unité Centrale de Traitement) avec CU (Unité de Contrôle) et ALU (Unité Arithmétique & Logique)
- MU (Unité de Mémoire)
- Input and Output Devices : Périphériques d'Entrée et Sortie
Les GPU sont généralement considérés comme des périphériques d'Entrée/Sortie. Comme la plupart des périphériques installés dans les machines, ils exploitent un bus d'interconnexion PCI ou PCI Express.
Pour récupérer la liste des périphériques PCI, utilisez la commande lspci -nn. A l'intérieur d'une longue liste apparaissent quelques périphériques VGA ou 3D. Ce sont les périphériques GPU ou GPGPU.
Voici une sortie de la commande lspci -nn | egrep '(VGA|3D)' :
3b:00.0 VGA compatible controller [0300]: NVIDIA Corporation GP102 [GeForce GTX 1080 Ti] [10de:1b06] (rev a1) a1:00.0 VGA compatible controller [0300]: NVIDIA Corporation GK107GL [Quadro K420] [10de:0ff3] (rev a1)
- Combien de périphériques VGA sont listés ?
- Combien de périphériques 3D sont listés ?
- Récupérez le modèle du circuit de GPU, dans son nom étendu.
- Récupérez sur le web les informations suivantes pour chaque GPU :
- le nombre d'unités de calcul (les “cuda cores” ou les “stream processors”)
- la fréquence de base des coeurs de calcul
- la fréquence de la mémoire
La (presque) totalité des stations de travail contiennent des cartes Nvidia.
Dans les systèmes Posix (Unix dans le langage courant), tout est fichier. Les informations sur les circuits Nvidia et leur découverte par le système d'exploitation peuvent être récupérées avec un grep dans la commande dmesg.
Si le démarrage de la machine n'est pas trop ancien, vous disposez des informations comparables aux suivantes :
[ 19.545688] NVRM: The NVIDIA GPU 0000:82:00.0 (PCI ID: 10de:1b06)
NVRM: NVIDIA Linux driver release. Please see 'Appendix
NVRM: A - Supported NVIDIA GPU Products' in this release's
NVRM: at www.nvidia.com.
[ 19.545903] nvidia: probe of 0000:82:00.0 failed with error -1
[ 19.546254] NVRM: The NVIDIA probe routine failed for 1 device(s).
[ 19.546491] NVRM: None of the NVIDIA graphics adapters were initialized!
[ 19.782970] nvidia-nvlink: Nvlink Core is being initialized, major device number 244
[ 19.783084] NVRM: loading NVIDIA UNIX x86_64 Kernel Module 375.66 Mon May 1 15:29:16 PDT 2017 (using threaded interrupts)
[ 19.814046] nvidia-modeset: Loading NVIDIA Kernel Mode Setting Driver for UNIX platforms 375.66 Mon May 1 14:33:30 PDT 2017
[ 20.264453] [drm] [nvidia-drm] [GPU ID 0x00008200] Loading driver
[ 23.360807] input: HDA NVidia HDMI/DP,pcm=3 as /devices/pci0000:80/0000:80:02.0/0000:82:00.1/sound/card2/input19
[ 23.360885] input: HDA NVidia HDMI/DP,pcm=7 as /devices/pci0000:80/0000:80:02.0/0000:82:00.1/sound/card2/input20
[ 23.360996] input: HDA NVidia HDMI/DP,pcm=8 as /devices/pci0000:80/0000:80:02.0/0000:82:00.1/sound/card2/input21
[ 23.361065] input: HDA NVidia HDMI/DP,pcm=9 as /devices/pci0000:80/0000:80:02.0/0000:82:00.1/sound/card2/input22
[ 32.896510] [drm] [nvidia-drm] [GPU ID 0x00008200] Unloading driver
[ 32.935658] nvidia-modeset: Unloading
[ 32.967939] nvidia-nvlink: Unregistered the Nvlink Core, major device number 244
[ 33.034671] nvidia-nvlink: Nvlink Core is being initialized, major device number 244
[ 33.034724] NVRM: loading NVIDIA UNIX x86_64 Kernel Module 375.66 Mon May 1 15:29:16 PDT 2017 (using threaded interrupts)
[ 33.275804] nvidia-nvlink: Unregistered the Nvlink Core, major device number 244
[ 33.993460] nvidia-nvlink: Nvlink Core is being initialized, major device number 244
[ 33.993486] NVRM: loading NVIDIA UNIX x86_64 Kernel Module 375.66 Mon May 1 15:29:16 PDT 2017 (using threaded interrupts)
[ 35.110461] nvidia-modeset: Loading NVIDIA Kernel Mode Setting Driver for UNIX platforms 375.66 Mon May 1 14:33:30 PDT 2017
[ 35.111628] nvidia-modeset: Allocated GPU:0 (GPU-ccc95482-6681-052e-eb30-20b138412b92) @ PCI:0000:82:00.0
[349272.210486] nvidia-uvm: Loaded the UVM driver in 8 mode, major device number 243
dmesg | grep -i nvidia- Quelle est la version de pilote chargée par le noyau ?
- Que représente, s'il existe, le périphérique
input: HDA NVidia? - Est-ce un périphérique graphique ?
Le lsmod offre la liste des modules chargés par le noyau. Ces modules sont de petits programmes dédiés au support d'une fontion très spécifique du noyau, le moteur du système d'exploitation. Le support d'un périphérique nécessite souvent plusieurs modules.
Un exemple de lsmod | grep nvidia sur une station de travail :
nvidia_uvm 778240 0 nvidia_drm 40960 4 nvidia_modeset 1044480 3 nvidia_drm nvidia 16797696 108 nvidia_modeset,nvidia_uvm ipmi_msghandler 49152 1 nvidia drm_kms_helper 155648 1 nvidia_drm drm 360448 7 nvidia_drm,drm_kms_helper
Nous voyons que 4 modules sont chargés. La dernière colonne (vide pour les deux premières lignes) liste les dépendances entre les modules. Ici nvidia_modeset and nvidia_uvm dépendent du module nvidia.
lsmod | grep nvidia
- Les informations sont-elles identiques à celles ci-dessus ? Caractère par caractère ?
Le périphérique apparaît également dans le dossier /dev (pour device), le dossier parent pour tous les périphériques.
Un ls -l /dev/nvidia* offre ce genre d'informations :
crw-rw-rw- 1 root root 195, 0 Jun 30 18:17 /dev/nvidia0 crw-rw-rw- 1 root root 195, 255 Jun 30 18:17 /dev/nvidiactl crw-rw-rw- 1 root root 195, 254 Jun 30 18:17 /dev/nvidia-modeset crw-rw-rw- 1 root root 243, 0 Jul 4 19:17 /dev/nvidia-uvm crw-rw-rw- 1 root root 243, 1 Jul 4 19:17 /dev/nvidia-uvm-tools
Vous pouvez voir que chacun peut accéder au périphérique, à la fois en lecture ET en écriture (le RW). Ici, vous avez un seul périphérique Nvidia, nvidia0. Sur une machine disposant de plusieurs périphériques Nvidia, nous aurions : nvidia0, nvidia1, etc…
ls -l /dev/* | grep -i nvidia
- Combien de
/dev/nvidia<number>avez-vous ? - Cette information est-elle cohérente avec les 3 précédentes ?
Nvidia présente des informations sur l'usage instantané de ses circuits avec la commande nvidia-smi. Cette commande peut aussi être exploitée pour régler certains paramètres de la GPU.
Voici un exemple de sortie de la commande nvidia-smi :
Fri Jul 7 07:46:56 2017
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 375.66 Driver Version: 375.66 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
|===============================+======================+======================|
| 0 GeForce GTX 108... Off | 0000:82:00.0 On | N/A |
| 23% 31C P8 10W / 250W | 35MiB / 11172MiB | 0% Default |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: GPU Memory |
| GPU PID Type Process name Usage |
|=============================================================================|
| 0 4108 G /usr/lib/xorg/Xorg 32MiB |
+-----------------------------------------------------------------------------+
Beaucoup d'informations sont disponibles sur cette sortie :
- version du pilote et du logiciel
nvidia-smi - l'identifiant de chaque GPU
- son nom
- sa localisation sur le bus PCIe
- sa vitesse de ventilateur
- sa température
- ses puissances : instantanée et maximale
- ses “occupations” mémoire : instantanée et maximale
- les processus les exploitant, leur consommation de mémoire et la GPU associée
nvidia-smi
- Identifiez les caractéristiques ci-dessus et comparer les éléments
- Combien de processus sont-ils listés ?
Comme nous l'avons vu dans l'introduction sur la GPU, leur programmation peut-être réalisée par différentes voies. La première, pour les périphériques Nvidia, est d'utiliser l'environnement CUDA. Le problème sera qu'il est impossible de réexploiter votre programme sur une autre plate-forme (une CPU) ou la comparer avec d'autres GPU. OpenCL reste une approche beaucoup plus polyvalente !
Sur les stations du CBP, la majorité des implémentations de OpenCL sont disponibles, autant sur CPU que sur GPU.
La commande clinfo récupère des informations liées à tous les périphériques OpenCL disponibles.
Pour récupérer une sortie compacte, utilisez clinfo '-l' .
Tous les périphériques OpenCL sont présentés suivant une hiérarchie plateforme/périphérique (Platform/Device).
Voici une sortie de clinfo '-l' pour une des stations de travail :
Platform #0: AMD Accelerated Parallel Processing `-- Device #0: Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz Platform #1: Portable Computing Language `-- Device #0: pthread-Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz Platform #2: NVIDIA CUDA +-- Device #0: GeForce GTX 1080 Ti `-- Device #1: Quadro K420 Platform #3: Intel(R) OpenCL `-- Device #0: Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz
#0,#0AMD Accelerated Parallel Processing : implémentation CPU de AMD, la plus ancienne, très proche de OpenMP en performances#1,#0Portable Computing Language : implémentation CPU OpenSource. Pas vraiment efficace#2,#0Nvidia CUDA : implémentation CUDA de Nvidia, périphérique 0, une GeForce GTX 1080 Ti#2,#1Nvidia CUDA : implémentation CUDA de Nvidia, périphérique 1, une Quadro K420#3,#0Intel(R) OpenCL : implémentation CPU Intel, plutôt très efficace
Ainsi, dans cette machine, 5 périphériques OpenCL sont accessibles, 3 permettent de s'adresser au processeur (vu pour le coup comme un périphérique) et 2 sont des GPU Nvidia.
clinfo -l
- Identifiez et comparez votre sortie avec la liste ci-dessus
- De combien de périphériques graphiques disposez-vous ?
L'appel de la commande clinfo fournit également de nombreuses informations. Cependant, il est impossible avec cette commande de ne récupérer les informations que d'un seul périphérique : la commande egrep permet alors de restreindre seulement certains attributs, par exemple Platform Name,Device Name,Max compute,Max clock
Sur la plateforme précédente, la commande clinfo | egrep '(Platform Name|Device Name|Max compute|Max clock)' offre comme sortie:
Platform Name AMD Accelerated Parallel Processing Platform Name Portable Computing Language Platform Name NVIDIA CUDA Platform Name Intel(R) OpenCL Platform Name AMD Accelerated Parallel Processing Device Name Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz Max compute units 16 Max clock frequency 1200MHz Platform Name Portable Computing Language Device Name pthread-Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz Max compute units 16 Max clock frequency 3501MHz Platform Name NVIDIA CUDA Device Name GeForce GTX 1080 Ti Max compute units 28 Max clock frequency 1582MHz Device Name Quadro K420 Max compute units 1 Max clock frequency 875MHz Platform Name Intel(R) OpenCL Device Name Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz Max compute units 16 Max clock frequency 3500MHz
Nous distinguons bien les éléments des 5 périphériques OpenCL déjà identifiés au-dessus (3 pour les 3 implémentations de CPU, respectivement d'AMD, PortableCL et Intel) et les deux GPU Nvidia (GTX 1080 Ti et Quadro K420).
Nous constatons par exemple que les nombres d'unités de traitement sont identiques pour les implémentations CPU (16) mais que leurs fréquences ne le sont pas (1200, 3501, 3500 MHz).
L'implémentation AMD récupère, elle, la fréquence instantanée, et les deux autres la fréquence maximale.
Pour les GPU, nous constatons que les fréquences sont bien inférieures à celles des GPU (1582 et 875 MHz).
Quant aux nombres d'unités de calcul (compute units), la première en dispose de 28 et la seconde de 1. Il sera donc intéressant de comparer ces valeurs par rapport aux valeurs trouvables dans les spécifications constructeur.
La notion d'unité de traitement (compute unit) pour les CPU n'est pas la même pour les GPU:
- pour les CPU, c'est généralement le produit du nombre de coeurs physiques et du nombre de threads
- pour les GPU, c'est le nombre de macro-unités de traitement : unité SM (pour Stream multiprocessor) chez Nvidia, unité CU (pour Compute Unit) chez AMD/ATI.
Ces unités de traitement disposent (autant pour les GPU que les CPU) d'unités arithmétiques et logiques (Arithmetic and Login Unit) lesquelles sont vraiment en charge du traitement des opérations.
Ainsi, le nombre d'ALU dans chaque Compute Unit varie de 64 à 192 selon les générations de GPU. Ainsi, pour le GPU ci-dessus GTX 1080 Ti, le nombre de Compute Unit mentionné est 28, et le nombre d'ALU (appelé également cuda core par Nvidia) est de 3584 soit 28*128. Le schéma du constructeur du circuit GP102 suivant est trompeur : en fait, il dispose de 30 unités SM, mais sur un GP102, seuls 28 sont activés.

clinfo
- Comparez les informations entre les implémentations CPU. Pourquoi ces différences ?
- Comparez le nombre d'unités de traitement des CPU avec celles du Web : Ark d'Intel
- Comparez le nombre d'unités de traitement des GPU avec celles du Web : site spécifications de Nvidia ou Wikipedia
- Comparez les fréquences identifiées avec celles trouvées sur le Web.
- Retrouvez-vous une cohérence entre le nombre de Compute Units et le nombre de cuda cores ?
- Combien de cuda cores contient chaque Compute Unit ?
Il est aussi possible de choisir quelle GPU Nvidia exploiter avec la variable d'environnement CUDA_VISIBLE_DEVICES. Il existe deux manières de l'exploiter :
- en préfixant la commande à exécuter (ou son programme) par
CUDA_VISIBLE_DEVICES=#GPU - en exportant la variable de manière permanente avec :
export CUDA_VISIBLE_DEVICES=#GPU
La commande nvidia-smi offrait une liste de périphériques Nvidia identifiés mais les ID donnés sont dans l'ordre inverse de celui exigé par CUDA_VISIBLE_DEVICES. Par exemple, nvidia-smi donne comme ID les nombres 0 et 1.
# N'exploiter que la GPU identifie #0 avec nvidia-smi CUDA_VISIBLE_DEVICES=1 <MonProgramme> # N'exploiter que la GPU identifie #1 avec nvidia-smi CUDA_VISIBLE_DEVICES=0 <MonProgramme> # Exploiter les GPUs identifies #0 et #1 avec nvidia-smi CUDA_VISIBLE_DEVICES=0,1 <MonProgramme> # N'exploiter aucune GPU CUDA_VISIBLE_DEVICES='' <MonProgramme>
clinfo -l préfixée de CUDA_VISIBLE_DEVICES
- Mettez
CUDA_VISIBLE_DEVICES=0 clinfo -let observez la sortie - Mettez
CUDA_VISIBLE_DEVICES=1 clinfo -let observez la sortie - Mettez
CUDA_VISIBLE_DEVICES=0,1 clinfo -let observez la sortie - Mettez
CUDA_VISIBLE_DEVICES=\'\' clinfo -let observez la sortie - Avez-vous constaté la sélection des différents périphériques ?
Durant toutes les séances de travaux pratiques, l'accent sera mis sur la sollicitation de ressources matérielles, CPU ou GPU, lors des exécutions. Pour avoir une idée des ressources exploitées en temps réel sur la machine sollicitée, il est intéressant d'exploiter les commandes dstat et nvidia-smi (déjà connue) dans deux terminaux sur votre bureau à distance avec les options -cim pour la première et dmon pour la seconde.
- Ouvrez un terminal, tapez
dstat -cimet observez la sortie - Détaillez à quoi servent les paramètres de sortie
c,ietm - Ouvrez un terminal, tapez
nvidia-smi dmonet observez la sortie - Détaillez à quoi sert l'option
dmon - Arrêtez l'exécution de la précédente avec
<Ctrl><C> - Relancez la commande précédente avec
-d 0ou-d 1 - Détaillez à quoi sert l'option
-dsuivie d'un entier
Récupération des sources
La (presque) totalité des outils exploités par le CBP pour comparer les CPU et les GPU se trouve dans le projet bench4gpu du Centre Blaise Pascal.
La récupération des sources est libre et se réalise par l'outil subversion :
svn checkout https://forge.cbp.ens-lyon.fr/svn/bench4gpu/
Dans ce dossier bench4gpu, il y a plusieurs dossiers :
BLAScontenant les dossiersxGEMMetxTRSV: tests exploitant toutes les implémentations de librairies BLASEpidevomath: un prototype d'implémentation sur GPU d'un projet (abandonné)FFTcontenant une première exploitation de cuFFT (en suspens)Ising: implémentations multiples du modèle d'Ising en Python (multiples parallélisations)NBody: implémentation en OpenCL d'un modèle N-Corps newtonienPi: implémentation multiples d'un Pi Monte CarloSplutter: un modèle depostillonneur mémoire, très utile pour évaluer les fonctions atomiquesTrouNoir: un exemple de portage de code de 1994, porté en C en 1997 puis en Python/OpenCL et Python/CUDA en 2019ETSN: les programmes corrigés associés à cette école ETSN 2022
De tous ces programmes, seuls ceux présents dans BLAS, NBody, Pi et ETSN seront exploités dans le cadre de ces travaux pratiques. Il est quand même conseillé de ne pas se précipiter sur les corrigés situés dans ETSN pour le déroulement de ces séances. Le no pain, no gain s'applique aussi dans l'apprentissage en informatique.
Première exploration de l'association Python et OpenCL
Basons-nous pour ce premier programme sur celui présenté sur la documentation officielle de PyOpenCL. Il se propose d'ajouter deux vecteurs a_np et b_np en un vecteur res_np.
#!/usr/bin/env python
import numpy as np
import pyopencl as cl
a_np = np.random.rand(50000).astype(np.float32)
b_np = np.random.rand(50000).astype(np.float32)
ctx = cl.create_some_context()
queue = cl.CommandQueue(ctx)
mf = cl.mem_flags
a_g = cl.Buffer(ctx, mf.READ_ONLY | mf.COPY_HOST_PTR, hostbuf=a_np)
b_g = cl.Buffer(ctx, mf.READ_ONLY | mf.COPY_HOST_PTR, hostbuf=b_np)
prg = cl.Program(ctx, """
__kernel void sum(
__global const float *a_g, __global const float *b_g, __global float *res_g)
{
int gid = get_global_id(0);
res_g[gid] = a_g[gid] + b_g[gid];
}
""").build()
res_g = cl.Buffer(ctx, mf.WRITE_ONLY, a_np.nbytes)
knl = prg.sum # Use this Kernel object for repeated calls
knl(queue, a_np.shape, None, a_g, b_g, res_g)
res_np = np.empty_like(a_np)
cl.enqueue_copy(queue, res_np, res_g)
# Check on CPU with Numpy:
print(res_np - (a_np + b_np))
print(np.linalg.norm(res_np - (a_np + b_np)))
assert np.allclose(res_np, a_np + b_np)
Un programme aussi simple, que nous allons peu à peu modifier, va nous servir de socle pour explorer de nombreuses facettes de Python en général et l'exploitation des GPU en particulier.
En cas de succès à l'exécution, sur une machine du CBP, par exemple la machine gtxtitan, le programme demande d'abord de choisir une plateforme :
Choose platform: [0] <pyopencl.Platform 'NVIDIA CUDA' at 0x288ab00> [1] <pyopencl.Platform 'Portable Computing Language' at 0x14b6a4754008> [2] <pyopencl.Platform 'AMD Accelerated Parallel Processing' at 0x14b69c602a18> [3] <pyopencl.Platform 'Intel(R) OpenCL' at 0x2a47810>
Puis un périphérique (s'il y en a plusieurs) :
Choose device(s): [0] <pyopencl.Device 'NVIDIA GeForce GTX TITAN' on 'NVIDIA CUDA' at 0x286dab0> [1] <pyopencl.Device 'Quadro K420' on 'NVIDIA CUDA' at 0x289ef90>
Une fois le choix effectué, la sortie est la suivante :
Set the environment variable PYOPENCL_CTX='0:0' to avoid being asked again. [0. 0. 0. ... 0. 0. 0.] 0.0
Ces choix et cette sortie nous rapportent au chapitre précédent lorsque nous avions exploité la commande clinfo -l. Nous avions vu que les périphériques OpenCL sont adressables par un tuple (plateforme,périphérique). Là, dans cet exemple, nous avons 2 périphériques Nvidia dont OpenCL nous donne les caractéristiques : GeForce GTX Titan et Quadro K420.
L'information importante ici est l'exploitation possible d'une variable d'environnement (PYOPENCL_CTX) pour sélectionner directement le périphérique à l'exécution. Par exemple, en préfixant l'exécution de PYOPENCL_CTX=0:1, nous sélectionnons la Quadro K420 et avec PYOPENCL_CTX=3 l'implémentation CPU de Intel Intel(R) OpenCL.
Nous verrons par la suite la possibilité de directement choisir le périphérique à l'intérieur même du code. Mais, cette opération étant un peu technique, nous nous contenterons de la variable d'environnement PYOPENCL_CTX préfixant la commande dans un premier temps.
- Exploitez un éditeur (par exemple gedit)
- Copiez/Coller le contenu du programme source précédent
- Enregistrez le source avec le nom
MySteps.py - Lancez le avec et jugez de l'exécution :
python MySteps.py - Lancez le avec et jugez de l'exécution :
python3 MySteps.py - Changez les droits d'exécution de
MySteps.py - Lancez le directement avec
./MySteps.py - En cas d'échec de lancement, modifiez
MySteps.py - Préfixez le lancement avec TOUTES les combinaisons de
PYOPENCL_CTX- par exemple :
PYOPENCL_CTX=X:Y ./MySteps.py
- Redirigez les sorties standards dans des fichiers
MySteps_XY.out(X,Y)sont définis comme les(plateforme,périphérique)- Attention, s'il n'existe qu'un
Xet pas deY, spécifiez uniquementX - Ex.:
PYOPENCL_CTX=X:Y ./MySteps.py > MySteps_XY.out 2>&1
Cet exemple de démonstration va être profondément modifié pour le transformer en un code matrice, un exemple de base qu'il sera possible d'exploiter pour toute nouvelle exploration. Sa documentation interne devra être assez explicite pour comprendre toutes les parties.
Nous commençons d'abord par copier ce programme comme la strate 0 de notre apprentissage : nous avons désormais un MySteps_0.py dans le même dossier. Comme premières opérations, nous allons :
- commenter le code en isolant les parties, notamment celles liées à OpenCL
- extraire le processus natif de calcul dans une fonction
NativeAddition - extraire le processus OpenCL complet dans une fonction
OpenCLAddition - appeler la fonction
NativeAdditionpour trouver le résultatres_np - appeler la fonction
OpenCLAdditionpour trouver le résultatres_cl - modifier les tests avec les résultats
res_npetres_cl
En ne modifiant pas encore les sorties du programme (stdin et stdout), nous nous assurons que nous n'avons pas perturbé cette réorganisation interne du programme.
Le travail suivant va être d'effectuer les opérations précédentes sur MySteps_0.py afin d'obtenir les mêmes sorties (au caractère près) que celles que nous avons déjà obtenues.
- Modifiez
MySteps_0.pysuivant les 6 spécifications ci-dessus - Exécutez le programme pour plusieurs périphériques
- Sauvez pour chaque exécution la sortie standard
- Comparez avec la commande
diffles sorties des exercices 2.1 et 2.2
L'étape suivante va permettre d'explorer le comportement du programme à la charge pour les différents types de périphériques, l'objectif étant de juger de l'intérêt du portage sur OpenCL en général ou sur GPU en particulier.
Le programme MySteps_1.py va intégrer les modifications suivantes :
- la possibilité de passer en argument à l'exécution la taille des vecteurs
- le temps d'exécution de la commande native
- le temps d'exécution de la commande en OpenCL
- une estimation de la vitesse d'exécution en natif pour différentes tailles
- une estimation de la vitesse d'exécution en OpenCL pour différentes tailles
- un ratio de performances entre mode natif et mode OpenCL
- la libération des mémoires réservées dans le bloc
OpenCLAddition
Deux exécutions consécutives sur GPU et CPU permettront ainsi de visualiser le gain entre une exécution sur CPU et GPU.
Le passage de l'argument au programme exploitera la librairie standard sys.
Le temps d'exécution se basera sur un mécanisme très simple : l'exploitation de 2 timers, le premier avant l'exécution, le second après l'exécution. Ce timer est la fonction time() de la librairie standard time.
Pour libérer l'espace réservé sur le périphérique avec les opérations Buffer, il suffit d'appeler la fonction .release() en suffixe de la variable.
Par exemple, à la commande PYOPENCL_CTX=0:0 ./MySteps_1.py 1048576, l'exécution répond :
Size of vectors set to 1048576 NativeRate: 899396014 OpenCLRate: 2873687 OpenCLvsNative ratio: 0.003195 [0. 0. 0. ... 0. 0. 0.] 0.0
Sur le CPU avec l'implémentation Intel, la commande PYOPENCL_CTX=3 ./MySteps_1.py 1048576, l'exécution répond :
NativeRate: 916259689 OpenCLRate: 2517963 OpenCLvsNative ratio: 0.002748 [0. 0. 0. ... 0. 0. 0.] 0.0
- Modifiez
MySteps_1.pysuivant les 7 spécifications ci-dessus - Exécutez le programme pour des tailles de vecteurs de 2^15 à 2^30
- sur la GPU la plus performante
- sur l'implémentation CPU la plus efficace : l'Intel
- Analysez dans quelles situations des problèmes de produisent :
- Raccordez ces difficultés aux spécifications matérielles
- Complétez un tableau avec ces résultats
- Concluez sur l'efficacité de OpenCL dans ce cas d'exploitation
Par exemple, sur la machine gtxtitan (déjà un peu ancienne), nous avons le tableau de résultats suivant :
Pour la GPU la plus performante, la GTX Titan avec 6GB de RAM :
| Size | NativeRate | OpenCLRate | Ratio |
|---|---|---|---|
| 32768 | 892460736 | 25740 | 0.000029 |
| 65536 | 1150116765 | 213780 | 0.000186 |
| 131072 | 1232636354 | 420621 | 0.000341 |
| 262144 | 1329518292 | 871262 | 0.000655 |
| 524288 | 1353245080 | 1675102 | 0.001238 |
| 1048576 | 1007340016 | 3765737 | 0.003738 |
| 2097152 | 793727939 | 6654994 | 0.008384 |
| 4194304 | 621127212 | 13609238 | 0.021911 |
| 8388608 | 637941219 | 22441689 | 0.035178 |
| 16777216 | 650779100 | 39385219 | 0.060520 |
| 33554432 | 652256978 | 59400977 | 0.091070 |
| 67108864 | 629199642 | 82412411 | 0.130980 |
| 134217728 | 653140112 | 100425544 | 0.153758 |
| 268435456 | 650963845 | 111139487 | 0.170731 |
| 536870912 | 650737914 | ||
| 1073741824 | 644699087 |
Les cases vides ne sont pas des oublis : pour ces exécutions sur gtxtitan, le programme a planté. Dans notre cas, le message suivant s'affichait
Traceback (most recent call last):
File "/home/equemene/bench4gpu/ETSN/./MySteps_1.py", line 71, in <module>
res_cl=OpenCLAddition(a_np,b_np)
File "/home/equemene/bench4gpu/ETSN/./MySteps_1.py", line 38, in OpenCLAddition
knl(queue, a_np.shape, None, a_g, b_g, res_g)
File "/usr/lib/python3/dist-packages/pyopencl/__init__.py", line 887, in kernel_call
return self._enqueue(self, queue, global_size, local_size, *args, **kwargs)
File "<generated code>", line 8, in enqueue_knl_sum
pyopencl._cl.MemoryError: clEnqueueNDRangeKernel failed: MEM_OBJECT_ALLOCATION_FAILURE
Son origine était assez explicite avec le MEM_OBJECT_ALLOCATION_FAILURE renseignant sur un problème mémoire ou plus précisément sur un dépassement de capacité d'allocation mémoire sur le périphérique. Dans cet exemple, la GPU sélectionnée est une GTX Titan avec 6GB de RAM. Notre programme planet dès que la taille des vecteurs dépasse 2^29 éléments soit 536870912. Si nous définissons 3 vecteurs composés de 536870912 flottants sur 32 bits, cela représente tout juste 6 GiB mais la GPU ne dispose que d'exactement 6083 MiB. Il en manque à peine, mais il en manque suffisamment !
Pour la CPU en implémentation Intel :
| Size | NativeRate | OpenCLRate | Ratio |
|---|---|---|---|
| 32768 | 803736570 | 48080 | 0.000060 |
| 65536 | 1179733506 | 229426 | 0.000194 |
| 131072 | 1235406323 | 464793 | 0.000376 |
| 262144 | 1321528398 | 798832 | 0.000604 |
| 524288 | 1369254829 | 1753352 | 0.001281 |
| 1048576 | 1010348382 | 3357138 | 0.003323 |
| 2097152 | 788462981 | 7530766 | 0.009551 |
| 4194304 | 608452462 | 15324510 | 0.025186 |
| 8388608 | 529925025 | 22077438 | 0.041661 |
| 16777216 | 652698625 | 44634386 | 0.068384 |
| 33554432 | 646735880 | 52990227 | 0.081935 |
| 67108864 | 657396843 | 92453020 | 0.140635 |
| 134217728 | 650361835 | 115909284 | 0.178223 |
| 268435456 | 650222491 | 138080711 | 0.212359 |
| 536870912 | 649709195 | 151511835 | 0.233199 |
| 1073741824 | 655357107 | 153145848 | 0.233683 |
Des résultats, il est possible de voir que, sur une opération aussi simple qu'une addition, dans aucune situation l'implémentation OpenCL n'apporte le moindre intérêt. L'exécution native en Python est toujours plus rapide d'un facteur 4 sur CPU et d'un facteur 6 sur GPU.
Pire, sur GPU, sur une GTX Titan avec 6GB de RAM, le programme a planté. Ce cas d'usage montre dès à présent ce qu'IL NE FAUT PAS FAIRE quand on exploite OpenCL en général et les GPU en particulier.
Toutefois, intéressante consolation, nous notons que, lorsque nous augmentons la taille de nos vecteurs, la performance ne cesse d'augmenter pour les implémentations OpenCL :
Pour juger de ces deux caractéristiques, nous allons non pas faire une simple addition de deux vacteurs mais une addition de ces deux vecteurs où chaque élément aura subi un ensemble d'opérations arithmétiques significatives.
Partons donc de notre programme précédent MySteps_1.py et copions le dans le programme MySteps_2.py.
Nous allons intégrer dans ce programme la fonction empilant successivement les 16 opérations suivantes : cos,arccos,sin,arcsin,tan,arctan,cosh,arccosh,sinh,arcsinh,tanh,arctanh,exp,log,sqrt et enfin élévation à la puissance 2. Comme notre générateur de nombres aléatoires tire entre 0 et 1, nous devrions retrouver notre nombre initial (modulo les approximations).
Cette fonction, nommée MySillyFunction devra être intégrée en Python natif et dans le noyau OpenCL. Lors de l'addition des deux vecteurs, nous appliquerons cette fonction aux éléments de a et b avant leur addition.
De plus, de manière à juger plus finement des opérations nécessaires en OpenCL, nous allons intrumenter la fonction d'appel pour juger du temps passé à l'exécution dans chacune d'elle.
Ainsi, les modifications du programme à effectuer sont les suivantes :
- dans la fonction
OpenCLAddition, rajouter des timers sur chaque opération - dans la fonction précédente, préfixez l'appel du noyau OpenCL par la variable
CallCL - dans la fonction précédente, rajoutez la ligne
CallCL.wait()la ligne sous la ligne précédente - intégrer la fonction
MySillyFunctionen python avec les 16 opérations suivant la liste ci-dessus- exploiter au besoin la documentation Python de la librairie numpy
- rajouter la fonction
NativeSillyAdditionappliquantMySillyFunctiondans le programme - intégrer la fonction
MySillyFunctiondans le noyau OpenCL avec les 16 opérations- exploiter au besoin la carte de référence OpenCL
- rajouter la fonction
sillysumsur la base desumdans le noyau OpenCL - rajouter la fonction
OpenCLSillyAdditionsur la base deOpenCLAdditiondans le programme
- Modifiez
MySteps_2.pysuivant les 8 spécifications ci-dessus - Exécutez le programme pour une taille de 32 (soit 2^5)
- sur la GPU la plus performante
- sur l'implémentation CPU la plus efficace : l'Intel
- Sauvegardez la sortie des deux exécutions précédentes
- Reexécutez les deux exécutions précédentes
- Sauvegardez la sortie des deux exécutions
- Que constatez-vous sur la durée de la synthèse OpenCL
- Exécutez le programme pour des tailles de vecteurs de 32 à 33554432
- sur la GPU la plus performante
- sur l'implémentation CPU la plus efficace : l'Intel
- Analysez dans quelles situations des problèmes de produisent
- Complétez un tableau avec ces résultats
Le premier problème rencontré lors de l'exécution génère les lignes comparables à :
Traceback (most recent call last):
File "/home/equemene/bench4gpu/ETSN/./MySteps_2.py", line 189, in <module>
assert np.allclose(res_np, res_cl)
AssertionError
Cette erreur provient du contrôle numpy.allclose du programme originel sur la comparaison entre résultats en mode natif et OpenCL. Comme le budget d'erreur est dépassé, une exception est levée. Etant donné l'accumulation des fonctions et que nous travaillons (pour l'instant) sur des nombres flottants sur 32 bits, entre 0 et 1, une erreur de inférieur à 1e-6 reste acceptable, mais il faut considérer qu'avec un grand nombre d'éléments, l'erreur cumulée devient significative sur l'ensemble du vecteur. Commenter cette ligne sera salutaire dans la suite.
Sur la comparaison entre les durées de synthèse OpenCL, nous constatons que la première exécution est toujours plus longue que la seconde. Sur notre machine référence, nous passons de 0.636s à 0.017s sur GPU (facteur 37) et de 0.1 à 0.018 (facteur 5). Cette différence vient du fait qu'entre les exécutions, les noyaux OpenCL n'ont pas changé : il n'y a pas lieu de refaire la synthèse des noyaux pour chaque périphérique. Ces éléments sont stockés dans $HOME/.cache/pyopencl. Il est donc nécessaire, sur de très gros noyaux OpenCL ou dans des tests de métrologie, de regarder ces temps de synthèse face aux temps d'exécution des noyaux.
Par exemple, sur la machine gtxtitan (déjà un peu ancienne), nous avons le tableau de résultats suivant :
Pour la GPU la plus performante, la GTX Titan avec 6GB de RAM :
| Size | NativeRate | OpenCLRate | Ratio |
|---|---|---|---|
| 32 | 248551 | 83 | 0.000334 |
| 64 | 429496 | 207 | 0.000482 |
| 128 | 662803 | 407 | 0.000614 |
| 256 | 842811 | 802 | 0.000952 |
| 512 | 923648 | 1668 | 0.001806 |
| 1024 | 1087884 | 3351 | 0.003080 |
| 2048 | 1140761 | 6712 | 0.005884 |
| 4096 | 1177025 | 13102 | 0.011131 |
| 8192 | 1210276 | 26014 | 0.021494 |
| 16384 | 1225470 | 60982 | 0.049762 |
| 32768 | 1220627 | 101652 | 0.083279 |
| 65536 | 1217372 | 215666 | 0.177157 |
| 131072 | 1232780 | 414668 | 0.336368 |
| 262144 | 1231938 | 883214 | 0.716931 |
| 524288 | 1374541 | 1889005 | 1.374281 |
| 1048576 | 1535449 | 3529675 | 2.298790 |
| 2097152 | 1523263 | 6720366 | 4.411823 |
| 4194304 | 1473851 | 12703168 | 8.619031 |
| 8388608 | 1479566 | 21404615 | 14.466820 |
| 16777216 | 1482238 | 36276007 | 24.473807 |
| 33554432 | 1484349 | 52485826 | 35.359492 |
Pour la CPU en implémentation Intel :
| Size | NativeRate | OpenCLRate | Ratio |
|---|---|---|---|
| 32 | 280790 | 98 | 0.000349 |
| 64 | 426765 | 243 | 0.000569 |
| 128 | 627919 | 435 | 0.000693 |
| 256 | 886657 | 936 | 0.001056 |
| 512 | 953166 | 1837 | 0.001927 |
| 1024 | 1082128 | 3099 | 0.002864 |
| 2048 | 1157829 | 6770 | 0.005847 |
| 4096 | 1183023 | 14486 | 0.012245 |
| 8192 | 1211043 | 27500 | 0.022708 |
| 16384 | 1228735 | 55910 | 0.045502 |
| 32768 | 1217685 | 101244 | 0.083145 |
| 65536 | 1222027 | 239095 | 0.195654 |
| 131072 | 1228707 | 410382 | 0.333995 |
| 262144 | 1231937 | 815420 | 0.661901 |
| 524288 | 1344654 | 1754317 | 1.304661 |
| 1048576 | 1318155 | 3223043 | 2.445117 |
| 2097152 | 1478456 | 6306681 | 4.265721 |
| 4194304 | 1527815 | 9490882 | 6.212062 |
| 8388608 | 1484125 | 14247142 | 9.599691 |
| 16777216 | 1482704 | 19512883 | 13.160336 |
| 33554432 | 1474004 | 22517796 | 15.276618 |
Nous constatons que le gain du passage en OpenCL est significatif, autant sur CPU que sur GPU, si la taille des objets approche le million. Nous avons une accélération de 15 pour le CPU et de 35 sur GPU. En augmentant la charge très significativement (par exemple en n'appelant pas seulement une fois MySillyFunction mais 4 fois à la suite, le gain sur CPU passe à 21 tandis qu'il dépasse les 127 sur cette GPU !
De plus, quand nous regardons les durées d'exécution des noyaux en OpenCL, elles sont presque marginales. Ainsi, pour qu'une exécution OpenCL soit efficace, il faudra veiller à ce que le temps d'exécution soit bien supérieur aux autres durées telles que les transferts de données entre hôte et périphérique ou l'initialisation du périphérique de calcul. Le programme PiXPU.py illustre de manière parfaite cet équilibre à établir sur le nombre de tâches concurrentielles à lancer et la profondeur calculatoire (ou l'intensité arithmétique) de chaque noyau.
Un intermède CUDA et son implémentation PyCUDA
Nvidia a ressenti tôt la nécessité d'offrir une abstraction de programmation simple pour ses GPU. Elle a même sorti cg-toolkit dès 2002. Il faudra attendre l'été 2007 pour un langage complet, seulement limité à quelques GPU de sa gamme.
Aujourd'hui, CUDA est omniprésent dans les librairies du constructeur mais aussi dans l'immense majorité des autres développements. Cependant, son problème vient de l'adhérence au constructeur : CUDA ne sert QUE pour Nvidia. Nous verrons que CUDA a aussi d'autres inconvénient, mais à l'usage.
L'impressionnant Andreas Kloeckner a aussi développé, en plus de PyOpenCL, PyCUDA pour exploiter CUDA à travers Python avec des approches : c'est PyCUDA.
L'exemple de la page précédente ressemble fortement à celui que nous modifions depuis le début de nos travaux pratiques. Nous allons l'exploiter pour intégrer cette implémentation CUDA dans notre programme MySteps_3.py (copie de MySteps_2.py).
Les modifications du programme MySteps_3.py sont les suivantes :
- créer une fonction Python
CudaAddition - intégrer les lignes de l'exemple de PyCUDA notamment
- l'appel des librairies Python
- le noyau CUDA où la multiplication a été remplacée par l'addition
- la création du vecteur destination
- l'appel de l'addition
- entourer avec une exception le
allclose- cette précaution permet d'empêcher un plantage
- dupliquer et adapter à CUDA les éléments de contrôle de cohérence des résultats
- Modifiez
MySteps_3.pysuivant les 3 spécifications ci-dessus - Exécutez le programme pour des tailles de vecteurs de 32 à 32768
- Analysez dans quelles situations des problèmes de produisent
- Raccordez ces difficultés aux spécifications matérielles
- Complétez un tableau avec ces résultats
- Concluez sur l'efficacité de CUDA dans ce cas d'exploitation
| Size | NativeRate | OpenCL Rate | CUDA Rate |
|---|---|---|---|
| 32 | 2982616 | 84 | 24 |
| 64 | 5592405 | 196 | 70 |
| 128 | 12485370 | 404 | 138 |
| 256 | 21913098 | 789 | 270 |
| 512 | 45691141 | 1652 | 535 |
| 1024 | 84215045 | 3153 | 1143 |
| 2048 | 156180628 | 6097 | |
| 4096 | 286331153 | 14923 | |
| 8192 | 483939977 | 25544 | |
| 16384 | 694136128 | 49892 | |
| 32768 | 947854851 | 101677 |
Normalement, si l'implémentation a été correcte, la partie CUDA fonctionne pour les tailles de vecteurs inférieures ou égales à 1024… Cette limitation est en fait dûe à une mauvaise utilisation de CUDA. En effet, CUDA (et dans une moindre mesure OpenCL) comporte 2 étages de parallélisation. Sous OpenCL, ces étages sont les Work Items et les Threads. Sous CUDA, ces étages sont les Blocks et les Threads. Hors, dans les deux approches OpenCL et CUDA, l'étage de parallélisation Threads est l'étage le plus fin, destiné à paralléliser des exécutions éponymes de la programmation parallèle. Mais, comme dans leurs implémentations sur processeurs, la parallélisation par Threads exige une “synchronisation”. Sous les implémentations CUDA et OpenCL, le nombre de threads maximal sollicitable dans un appel est seulement 1024 !
Cette limitation de 1024 Threads entre en contradiction avec le cadre d'utilisation présenté sur les GPU qui veut que le nombre de tâches équivalentes à exécuter est de l'ordre d'au moins plusieurs dizaines de milliers. Donc, il ne faut pas, dans un premier temps, exploiter les Threads en CUDA mais les Blocks.
Il faudra donc modifier le programme MySteps_4.py (copie de MySteps_3.py fonctionnel mais inefficace) pour exploiter les Blocks. Les modifications sont les suivantes :
- remplacer
threadIdxparblockIdxdans le noyau CUDA - remplacer dans l'appel de
sum:block=(a_np.size,1,1)parblock=(1,1,1) - remplacer dans l'appel de
sum:grid=(1,1)pargrid=(a_np.size)
- Modifiez
MySteps_4.pysuivant les 3 spécifications ci-dessus - Exécutez le programme pour des tailles de vecteurs de 32768 à 268435456
- Analysez dans quelles situations des problèmes de produisent
- Raccordez ces difficultés aux spécifications matérielles
- Complétez un tableau avec ces résultats
- Concluez sur l'efficacité de CUDA dans ce cas d'exploitation
| Size | NativeRate | OpenCL Rate | CUDA Rate |
|---|---|---|---|
| 32768 | 910191744 | 93081 | 31182 |
| 65536 | 1150116765 | 199750 | 71033 |
| 131072 | 1221679586 | 455109 | 165674 |
| 262144 | 1337605386 | 793248 | 280624 |
| 524288 | 1397980454 | 1572131 | 570096 |
| 1048576 | 1069824011 | 3060792 | 1116513 |
| 2097152 | 775327723 | 5831761 | 2246784 |
| 4194304 | 517143454 | 11881835 | 4384631 |
| 8388608 | 642015438 | 24217467 | 8813252 |
| 16777216 | 629968524 | 39845498 | 17001502 |
| 33554432 | 645555196 | 57715607 | 29982747 |
| 67108864 | 650246900 | 80830493 | 50612097 |
| 134217728 | 654420232 | 99003136 | 75783432 |
| 268435456 | 656531263 | 111858992 | 91297615 |
Nous constatons normalement, avec la sollicitation des blocks et plus des threads, l'implémentation CUDA fonctionne quelle que soit la taille sollicitée. L'implémentation CUDA rattrape l'OpenCL sans jamais la dépasser mais elle reste indigente en comparaison avec la méthode native, mais nous avons déjà vu pourquoi : problème de complexité arithmétique.
Nous allons donc, comme pour OpenCL, augmenter l'intensité arithmétique du traitement en rajoutant l'implémentation CUDA de notre fonction MySillyFunction ajoutée à chacun des termes des vecteurs avant leur addition.
Pour il convient de modifier le code MySteps_5.py (copie de MySteps_4.py) de la manière suivante :
- copier l'implémentation PyCUDA
CUDAAdditionenCUDASillyAddition- cette nouvelle fonction Python sera à modifier pour la suite
- rajouter la fonction interne
MySillyFunctiondans le noyau CUDA- une fonction interne doit être préfixée par
device
- rajouter la fonction
sillysumappelée par Python dans le noyau CUDA - rajouter la synthèse de la fonction
sillysumcomparable àsum - modifier l'appel de la fonction PyCUDA de
sumensillysum - intrumenter temporellement chaque ligne de
CUDASillyAddition - modifier les appels de fonction
AdditionenSillyAddition- pour les 3 implémentations
Native,OpenCLetCUDA
- Modifiez
MySteps_5.pysuivant les 7 spécifications ci-dessus - Exécutez le programme pour des tailles de vecteurs de 32768 à 268435456
- Complétez un tableau avec ces résultats
- Concluez sur l'efficacité de CUDA dans ce cas d'exploitation
| Size | NativeRate | OpenCL Rate | CUDA Rate | OpenCL ratio | CUDA ratio |
|---|---|---|---|---|---|
| 32768 | 1220822 | 104351 | 29276 | 0.085476 | 0.023981 |
| 65536 | 1220648 | 209305 | 69271 | 0.171470 | 0.056749 |
| 131072 | 1230476 | 393187 | 140255 | 0.319541 | 0.113984 |
| 262144 | 1248695 | 884181 | 298047 | 0.708084 | 0.238687 |
| 524288 | 1447905 | 1790726 | 574288 | 1.236770 | 0.396634 |
| 1048576 | 1444680 | 3401922 | 1118288 | 2.354793 | 0.774073 |
| 2097152 | 1484030 | 6988430 | 2056560 | 4.709089 | 1.385794 |
| 4194304 | 1525560 | 13208467 | 3606081 | 8.658110 | 2.363775 |
| 8388608 | 1478514 | 22047721 | 5106220 | 14.912081 | 3.453616 |
| 16777216 | 1484119 | 37736167 | 7228717 | 25.426645 | 4.870713 |
| 33554432 | 1484581 | 54005921 | 9291681 | 36.377888 | 6.258790 |
| 67108864 | 1484264 | 75264794 | 10552401 | 50.708495 | 7.109518 |
| 134217728 | 1486942 | 85222066 | 11352687 | 57.313645 | 7.634923 |
| 268435456 | 1485632 | 102563944 | 12149328 | 69.037247 | 8.177885 |
Les gains sont substantiels en CUDA mais restent quand même bien en dessous de OpenCL. Pour augmenter l'efficacité de CUDA, il conviendra d'augmenter la complexité arithmétique de manière très substantielle. Par exemple, en multipliant par 16 cette complexité (en appelant par exemple 16 fois successivement cette fonction MySillyFunction), le NativeRate se divise par 16 mais le OpenCLRate ne se divise que par 2. L'implémentation CUDA, quand à elle, augmente de 60% !
Pour conclure sue ce petit intermède CUDA se trouvent les programmes MySteps_5b.py et MySteps_5c.py dérivés de MySteps_5.py :
MySteps_5b.py: intègre une utilisation hybride des Blocks et des ThreadsMySteps_5c.py: augmente la complexité arithmétique d'un facteur 16
Implémenter une fonction "coûteuse", la Transformée de Fourier
L'objectif ici n'est pas de concurrencer une implémentation de la FFT, par ailleurs très bien implémentée en Python natif. Le dessein est plutôt d'illustrer l'exploitation d'un des programmes précédents comme matrice de manière à construire ce programme.
La Transformée de Fourier discrète est omniprésente en traitement du signal. Elle permet notamment des opérations de filtrage plus efficaces que les convolutions directes.
Le lien Wikipedia contient tout ce qui est nécessaire à l'implémentation de votre propre TF d'abord en Python “naïf”, puis en Python Numpy, ensuite en Python PyOpenCL et enfin en Python CUDA.
Comme le veut la tradition, la DFT s'applique sur un vecteur complexe comprenant donc parties réelle et imaginaire et offre un résultat dans l'espace complexe. Les vecteurs a_np et b_np seront donc respectivement les parties réelles et imaginaires de notre vecteur d'entrée.
Pour cela, nous partons de MySteps_5.py que nous copions en MyDFT_1.py. Nous pouvons dans un premier temps commenter toutes les parties que nous ne comptons pas exploiter, ou simplement ne pas les appeler dans la fin du programme.
Pour des valeurs réelles et imaginaires fixées à 1 dans le vecteur complexe, les valeurs théoriques de leur DFT sont :
- identiques pour les parties réelles et imaginaires
- égales à 1 pour le premier élément
- égales à 0 pour les autres termes
Ainsi, pour implémenter une DFT “naïve”, nous devons :
- commenter toutes les parties inutiles du programme
MyDFT_1.py - initialiser les vecteurs
a_npetb_npà1 - initialiser les vecteurs
C_npetD_nprésultats (ou références) - créer une fonction Python
MyDFT- arguments
xety - résultats
XetY
- implémenter la DFT à base d'itérateurs
- appeler la fonction
MyDFTavec :- arguments
a_npetb_np - résultats
c_npetd_np
- imprimer la somme des différences normalisées
- entre
c_npetC_np - entre
d_npetD_np
Il sera alors possible d'estimer l'erreur numérique à ce calcul.
- Modifiez
MyDFT_1.pysuivant les 7 spécifications ci-dessus - Exécutez le programme pour une taille de 16 et contrôler la cohérence
- Exécutez le programme pour des tailles de vecteurs de 16 à 4096
- Placez dans un tableau la performance
Si tout va bien, les vecteurs résultats présentent une valeur comparable à la taille du vecteur sur le premier élément et une valeur “proche” de 0 ailleurs. Pour une DFT appliquée sur un vecteur de 1024 éléments, la sortie est la suivante :
Size of vectors set to 1024 NativeRate: 23 Precision: 6.975449e-05 6.9193055e-05
La double-itération est particulièrement coûteuse en terme de calcul. La seconde implémentation va exploiter les fonctions broadcast de Numpy pour éviter cette double-boucle en la limitant à une seule boucle.
Pour cela, il est proposé de :
- copier la fonction
NumpyDFTsur le modèle deMyDFT - dans cette nouvelle fonction, réaliser les opérations suivantes :
- créer un vecteur
njcorrespondant à l'argument des cos et sin divisé par i- l'exploitation de
numpy.multiplyest suggérée
- créer l'élément
X[i]par l'enchaînement des opérations :- produit de cos(i*nj) à x
- produit de sin(i*nj) à x
- soustraction des deux résultats précédents
- somme de l'ensemble des éléments
- créer l'élément
Y[i]par l'enchaînement des opérations :- produit de sin(i*nj) à x
- produit de cos(i*nj) à x
- addition des deux résultats précédents
- somme de l'ensemble des éléments
- appeler la fonction
NumpyDFTavec les mêmes arguments - comparer les résultats entre les deux avec
linalg.norm
- Copiez le programme
MyDFT_1.pyenMyDFT_2.py - Modifiez
MyDFT_2.pysuivant les 7 spécifications ci-dessus - Exécutez le programme pour une taille de 1024 et contrôler la cohérence
- Exécutez le programme pour des tailles de vecteurs de 16 à 4096
- Placez dans un tableau la performance
Nous constatons que l'exploitation des fonctions broadcast est infiniment plus efficace que l'implémentation naïve. Cependant, une observation des résultats laisse un tantinet perplexe sur la précision des opération. En effet, pour une exécution sur des vecteurs de tail 1024, nous avons :
Size of vectors set to 1024 Performing naive implementation NativeRate: 23 Precision: 6.975449e-05 6.9193055e-05 Performing Numpy implementation NumpyRate: 8030 Precision: 0.08201215 0.0809835
Les résultats par la méthode naïve semblent être plus précis (attention cependant, nous avons forcé les calculs sur des flottants 32 bits). Cela suggère qu'un contrôle calculatoire est plus que jamais nécessaire, quelle que soit la méthode exploitée, en Python ou autre.
L'utilisation de Numba offre une possibilité de parallélisation comparable à OpenMP. Avec une directive préfixant la fonction et quelques modifications, il est possible (normalement simplement) de paralléliser l'exécution d'une boucle sur plusieurs coeurs voire envoyer l'exécution de la boucle sur un périphérique externe. Nous l'utiliserons que la parallélisation sur plusieurs coeurs.
Dans notre cas, il suffira de :
- importer la librairie numba :
import numba - préciser l'appel du décorateur sur CPU :
@numba.njit(parallel=True) - changer le domaine d'itération pour la boucle :
range()parnumba.prange()
- Copiez le programme
MyDFT_2.pyenMyDFT_3.pyet exploitez ce dernier - Copiez la fonction
NumpyDFTenNumbaDFT - Intégrez les deux lignes intégrant numba
- Dupliquez l'appel de
NumpyDFTpour appelerNumbaDFT - Rajoutez un comparateur de résultats avec le mode natif
- Exécutez le programme pour une taille de 1024 et contrôler la cohérence
- Exécutez le programme pour des tailles de vecteurs de 16 à 4096
- Placez dans un tableau la performance
Les résultats ont de quoi laisser effectivement perplexe… L'implémentation avec Numba semble plus lente que l'implémentation Numpy qu'elle exploite !
Size of vectors set to 1024 Performing naive implementation NativeRate: 22 Precision: 6.975449e-05 6.9193055e-05 Performing Numpy implementation NumpyRate: 8157 Precision: 0.08201215 0.0809835 Performing Numba implementation /usr/lib/python3/dist-packages/numba/np/ufunc/parallel.py:365: NumbaWarning: The TBB threading layer requires TBB version 2019.5 or later i.e., TBB_INTERFACE_VERSION >= 11005. Found TBB_INTERFACE_VERSION = 7001. The TBB threading layer is disabled. warnings.warn(problem) NumbaRate: 393 Precision: 0.065024495 0.059959255
Nous disposons également d'un message d'erreur mais pas vraiment grave… Ca fonctionne quand même ![]()
Pour l'implémentation OpenCL, la version “naïve” de l'implémentation va servir. Pour cela, il suffit de reprendre la définition de la méthode naïve et de l'implémenter en C dans un noyau OpenCL. A noter que Pi n'étant dans une variable définie, il faut explicitement la détailler dans le noyau OpenCL. Autre détail important : le cast. De manière a éviter tout effet de bord, il est fortement recommandé de caster les opérations dans la précision flottante souhaitée pour des opérations sur des indices entiers.
- Copiez le programme
MyDFT_3.pyenMyDFT_4.pyet exploitez ce dernier - Copiez la fonction python
OpenCLAdditionenOpenCLDFT - Sur la base de la fonction noyau
sum, créer la fonctionMyDFT - Intégrez la valeur de PI en début de noyau OpenCL
- Modifiez les allocations pour la sortie de la fontion OpenCL
MyDFT - Modifiez la synthèse du noyau OpenCL
- Modifiez l'exécution du noyau OpenCL avec
MyDFT - Adaptez les transferts de périphérique vers l'hôte
- Appelez la fonction
OpenCLDFTdans la routine - Inhibez l'implémentation “naïve” trop inefficace
- Exécutez le programme pour une taille de 1024 et contrôler la cohérence
- Exécutez le programme sur CPU pour des tailles de vecteurs de 64 à 65536
- Exécutez le programme sur GPU pour des tailles de vecteurs de 64 à 65536
- Placez dans un tableau la performance
Sur la base d'une DFT appliquée sur un vecteur complexe de 1024 éléments avec comme périphérique OpenCL l'implémentation Intel, nous avons la sortie suivante :
Size of vectors set to 1024 Performing Numpy implementation NumpyRate: 6282 Precision: 0.08201215 0.0809835 Performing Numba implementation /usr/lib/python3/dist-packages/numba/np/ufunc/parallel.py:365: NumbaWarning: The TBB threading layer requires TBB version 2019.5 or later i.e., TBB_INTERFACE_VERSION >= 11005. Found TBB_INTERFACE_VERSION = 7001. The TBB threading layer is disabled. warnings.warn(problem) NumbaRate: 356 Precision: 0.065024495 0.059959255 Copy from Host 2 Device : 0.000 Building kernels : 0.013 Allocation on Host for results : 0.000 Allocation on Device for results : 0.000 Synthesis of kernel : 0.005 Execution of kernel : 0.007 Copy from Device 2 Host : 0.000 OpenCLRate: 3306 Precision: 6.966685e-05 6.9132504e-05
La précision en OpenCL est comparable à la méthode native, bien meilleure que les méthodes Python Numpy ou Numba. La performance est en deça de la méthode Numpy. Par contre, dès que les vecteurs dépassent une certaine taille (8192 avec Numba et 2048 avec OpenCL), Numpy est largement battu.
Avec l'implémentation OpenCL Intel sur CPU :
| Size | NumpyRate | NumbaRate | OpenCL Rate |
|---|---|---|---|
| 64 | 15225 | 24 | 186 |
| 128 | 17045 | 55 | 477 |
| 256 | 14199 | 112 | 926 |
| 512 | 8361 | 218 | 1820 |
| 1024 | 7980 | 440 | 1550 |
| 2048 | 4308 | 865 | 7945 |
| 4096 | 2894 | 1626 | 12810 |
| 8192 | 1584 | 2565 | 18533 |
| 16384 | 852 | 2223 | 22087 |
| 32768 | 435 | 2143 | 16604 |
| 65536 | 221 | 1212 | 9497 |
Avec l'implémentation OpenCL sur GPU :
| Size | NumpyRate | NumbaRate | OpenCL Rate |
|---|---|---|---|
| 64 | 15117 | 25 | 204 |
| 128 | 14398 | 54 | 463 |
| 256 | 15201 | 111 | 948 |
| 512 | 8860 | 201 | 1866 |
| 1024 | 8061 | 441 | 3786 |
| 2048 | 4605 | 874 | 5968 |
| 4096 | 2892 | 1628 | 12852 |
| 8192 | 1617 | 2636 | 19731 |
| 16384 | 848 | 2884 | 24280 |
| 32768 | 433 | 2032 | 20077 |
| 65536 | 220 | 1217 | 11054 |
Reste maintenant l'implémentation CUDA sur la base de ce qui a déjà été fait dans l'exercice 3.4.
Il faudra, comme pour l'implémentation OpenCL, veiller à :
- intégrer la valeur de PI comme constante
- modifier les vecteurs en sortie (2 vecteurs)
- Copiez le programme
MyDFT_4.pyenMyDFT_5.pyet exploitez ce dernier - Copiez la fonction python
CUDAAdditionenCUDADFT - Sur la base de la fonction noyau
sum, créer la fonctionMyDFT - Intégrez la valeur de PI en début de noyau OpenCL
- Modifiez les allocations pour la sortie de la fontion CUDA
MyDFT - Modifiez la synthèse du noyau CUDA
- Modifiez l'exécution du noyau CUDA avec
MyDFT - Appelez la fonction
CUDADFTdans la routine - Exécutez le programme pour une taille de 1024 et contrôler la cohérence
- Exécutez le programme sur GPU pour des tailles de vecteurs de 64 à 65536
- Placez dans un tableau la performance
Pour l'exécution de la DFT sur vecteur complexe de 1024 éléments sur GPU, nous avons comme sortie :
Size of vectors set to 1024 Performing Numpy implementation NumpyRate: 6344 Precision: 0.08201215 0.0809835 Performing Numba implementation /usr/lib/python3/dist-packages/numba/np/ufunc/parallel.py:365: NumbaWarning: The TBB threading layer requires TBB version 2019.5 or later i.e., TBB_INTERFACE_VERSION >= 11005. Found TBB_INTERFACE_VERSION = 7001. The TBB threading layer is disabled. warnings.warn(problem) NumbaRate: 416 Precision: 0.065024495 0.059959255 Copy from Host 2 Device : 0.000 Building kernels : 0.010 Allocation on Host for results : 0.000 Allocation on Device for results : 0.000 Synthesis of kernel : 0.003 Execution of kernel : 0.007 Copy from Device 2 Host : 0.000 OpenCLRate: 3486 Precision: 6.966685e-05 6.9132504e-05 Definition of kernel : 0.018 Synthesis of kernel : 0.000 Allocation on Host for results : 0.000 Execution of kernel : 0.044 CUDARate: 6629 Precision: 6.966685e-05 6.9132504e-05
Nous constatons que le l'efficacité de CUDA est presque double de celle OpenCL.
Voyons si cette performance se confirme pour toutes les tailles de vecteurs.
| Size | NumpyRate | NumbaRate | OpenCL Rate | CUDA Rate |
|---|---|---|---|---|
| 64 | 15297 | 25 | 201 | 556 |
| 128 | 13792 | 51 | 466 | 1169 |
| 256 | 14692 | 112 | 926 | 2297 |
| 512 | 8837 | 210 | 1812 | 4248 |
| 1024 | 7335 | 431 | 3574 | 6653 |
| 2048 | 4592 | 865 | 7214 | 7368 |
| 4096 | 2753 | 1623 | 13253 | 6019 |
| 8192 | 1627 | 2577 | 21140 | 3538 |
| 16384 | 852 | 2829 | 24491 | 1835 |
| 32768 | 430 | 2135 | 11410 | 929 |
| 65536 | 221 | 1215 | 11048 | 466 |
Nous constatons que CUDA monte plus rapidement en charge que OpenCL lorsque la taille du problème augmente. Cependant, CUDA attend une limite pour une taille de 2048 puis régresse drastiquement ensuite alors que OpenCL sa progression jusqu'à une taille de 16384.
Pour CUDA, cela montre que nous sommes arrivés à saturation de l'exploitation du premier étage de parallélisme avec les blocks : il faut maintenant exploiter les threads de manière concomitante. L'exemple MyDFT_5b.py illustre cette exploitation hybride. Les résultats pour une exploitation de 1024 threads (donc une taille de vecteur complexe de 1024) parlent d'eux-mêmes :
| Size | NumpyRate | NumbaRate | OpenCL Rate | CUDA Rate |
|---|---|---|---|---|
| 1024 | 6387 | 422 | 3239 | 7480 |
| 2048 | 4707 | 877 | 7206 | 14011 |
| 4096 | 2968 | 1627 | 12147 | 22127 |
| 8192 | 1610 | 2620 | 19829 | 33377 |
| 16384 | 849 | 2888 | 25233 | 27880 |
| 32768 | 434 | 2106 | 18805 | 21061 |
| 65536 | 221 | 1214 | 11162 | 13446 |
Dans ce cas, CUDA est toujours plus performant que OpenCL mais la contrainte reste de pouvoir exploiter efficacement ces deux étages de parallélisme. Cette différence d'efficacité n'est pas systématique : nous réalisons d'abord qu'elle dépend du système considéré mais cela va également complètement dépendre de l'architecture interne de la GPU, donc sa génération, son nombre de coeurs CUDA, sa mémoire, etc…
L'exemple précédent était exécuté sur une GTX Titan avec circuit Kepler datant de 2013.
Sur une RTX 6000, la domination de Python/CUDA est plus nuancée :
| Size | NumpyRate | NumbaRate | OpenCL Rate | CUDA Rate |
|---|---|---|---|---|
| 1024 | 31353 | 823 | 3999 | 7795 |
| 2048 | 26627 | 1735 | 8738 | 13045 |
| 4096 | 27098 | 3298 | 15042 | 18896 |
| 8192 | 17416 | 5619 | 25359 | 25075 |
| 16384 | 9047 | 6585 | 40884 | 29655 |
| 32768 | 2414 | 5832 | 37860 | 32461 |
| 65536 | 838 | 3540 | 24963 | 33812 |
Quant à l'exploitation d'une carte professionnelle A100, les différences sont marquantes !
| Size | NumpyRate | NumbaRate | OpenCL Rate | CUDA Rate |
|---|---|---|---|---|
| 1024 | 37922 | 772 | 2042 | 1663 |
| 2048 | 35043 | 1743 | 6758 | 13978 |
| 4096 | 25283 | 3385 | 13559 | 25791 |
| 8192 | 14887 | 6171 | 25565 | 47268 |
| 16384 | 8440 | 9097 | 48969 | 76644 |
| 32768 | 2562 | 9036 | 85271 | 117726 |
| 65536 | 715 | 6252 | 117873 | 179320 |
En conclusion de cette partie, une approche progressive qui consiste de partir d'abord d'une implémentation “naïve” agnostique à tout langage, puis d'exploiter les spécificités des uns ou des autres (comme les broadcast Numpy ou la parallélisation par Numba), ensuite de construire avec Python/OpenCL un modèle qui s'exécutera partout (sur CPU ou GPU), enfin construire avec un Python/CUDA si le problème s'y prête, est une approche pertinente. A chaque étape, il est possible de s'arrêter si la performance est en accord avec son budget de développement.
Le choix du périphérique en OpenCL et CUDA
Dans le chapitre 1, nous avons vu qu'il était possible de choisir le périphérique CUDA en inhibant sa visibilité avec la variable d'environnement CUDA_VISIBLE_DEVICES. Seul le ou les périphériques sélectionnés étaient visibles. Cette méthode est cependant un peu brutale, surtout si nous souhaitons adresser plusieurs GPU dans notre exécution.
Dans le chapitre 2, nous avons vu que pour éviter d'avoir à spécifier le périphérique OpenCL, nous pouvions exploiter la variable d'environnement PYOPENCL_CTX. C'était effectivement utile mais nous n'avions pas l'assurance d'exécuter réellement sur ce périphérique sauf en regardant attentitivement les résultats des commandes htop ou nvidia-smi dmon'.
Les méthodes présentées dans la suite ont l'avantage d'être systématiques et donc pourront être exploitées dans n'importe quel programme PyOpenCL pour PyCUDA.
A cela s'ajoute également la possibilité d'ajouter des options au lancement du programme, notamment pour spécifier sa GPU. Dans les programmes de l'archive bench4gpu en Python, la majorité dispose d'une option -h permettant de voir les options ainsi que de lister les périphériques OpenCL ou CUDA détectés.
L'objectif est donc de reprendre notre exemple le plus abouti de notre DFT et d'y ajouter ces éléments. Pour cela, les programmes PiXPU.py et TrouNoir.py vont être explorés pour voir comment faire.
- Identifiez les lignes correspondant aux paramétrages par défaut
- Identifiez les lignes sur la découverte des périphériques OpenCL
- Identifiez les lignes sur la découverte des périphériques CUDA
- Identifiez les lignes de l'extraction des arguments d'entrées
- Identifiez les lignes de selection du périphérique OpenCL à l'exécution
- Identifiez les lignes de selection du périphérique CUDA à l'exécution
Une fois ces portions identifiées, la modification du programme MyDFT_6.py (copie de MyDFT_5.py) portera les éléments suivants :
- Intégrer l'option
–havec la présentation des périphériques OpenCL et CUDA - Fixer à 1024 la valeur par défaut du nombre de points
- Fixer à OpenCL la méthode par défaut d'exécution
- Fixer à 0 le premier périphérique OpenCL ou CUDA sollicité
- Sélectionner le nombre de points avec l'option
-s - Sélectionner le périphérique OpenCL ou CUDA (énumération directe) avec
-d - Sélectionner une exécution sous OpenCL ou CUDA avec l'option
-g
MyDFT_6.py- Supprimer la sélection initiale d'argument
- Inhiber pour l'instant l'exécution des fonctions
- Intégrez les 7 spécifications ci-dessus par de judicieux copier/coller de
PiXPU.py - Vérifiez l'option
-h
Ainsi, pour une sollification avec l'option -h, le programme sort :
./MySteps_6.py -g <CUDA/OpenCL> -s <SizeOfVector> -d <DeviceId> Informations about devices detected under OpenCL API: Device #0 from NVIDIA Corporation of type xPU : NVIDIA GeForce GTX TITAN Device #1 from NVIDIA Corporation of type xPU : Quadro K420 Device #2 from The pocl project of type xPU : pthread-Intel(R) Xeon(R) CPU E5-2620 0 @ 2.00GHz Device #3 from Advanced Micro Devices, Inc. of type xPU : Intel(R) Xeon(R) CPU E5-2620 0 @ 2.00GHz Device #4 from Intel(R) Corporation of type xPU : Intel(R) Xeon(R) CPU E5-2620 0 @ 2.00GHz Informations about devices detected under CUDA API: Device #0 of type GPU : NVIDIA GeForce GTX TITAN Device #1 of type GPU : Quadro K420
Maintenant, sur la base de l'exploration de PiXPU.py, il est temps de modifier les appels aux fonctions OpenCLDFT et CUDADFT dans le programme MyDFT_7.py (copie de MyDFT_6.py)
En regardant en détail la sélection du périphérique, elle est assez simple du moment que l'énumération des périphériques est réalisée. D'abord sur les plates-formes, ensuite sur les périphériques, avec une indentation jusqu'à trouver sonpériphérique.
Id=0
HasXPU=False
for platform in cl.get_platforms():
for device in platform.get_devices():
if Id==Device:
XPU=device
print("CPU/GPU selected: ",device.name.lstrip())
HasXPU=True
Id+=1
# print(Id)
if HasXPU==False:
print("No XPU #%i found in all of %i devices, sorry..." % (Device,Id-1))
sys.exit()
MyDFT_7.py- Libérez pour l'appel à la fonction
OpenCLDFT - Rajoutez le test exploitant la sélection OpenCL ou CUDA
- Modifiez l'appel de
OpenCLDFTpour intégrer le choix du périphérique - Modifiez la fonction
OpenCLDFTsur la base de fonctionMetropolisOpenCLdePiXPU.py - Exécutez le programme par défaut (sans option)
- Exécutez le programme sur la seconde GPU
Par défaut, la taille du vecteur complexe est 1024, le périphérique sollicité est 0 pour une utilisation en OpenCL. La sortie sur la machine ressemble à :
Device Selection : 0 GpuStyle used : OpenCL Size of complex vector : 1024 Device #0 from NVIDIA Corporation of type xPU : NVIDIA GeForce GTX TITAN Device #1 from NVIDIA Corporation of type xPU : Quadro K420 Device #2 from The pocl project of type xPU : pthread-Intel(R) Xeon(R) CPU E5-2620 0 @ 2.00GHz Device #3 from Advanced Micro Devices, Inc. of type xPU : Intel(R) Xeon(R) CPU E5-2620 0 @ 2.00GHz Device #4 from Intel(R) Corporation of type xPU : Intel(R) Xeon(R) CPU E5-2620 0 @ 2.00GHz CPU/GPU selected: NVIDIA GeForce GTX TITAN Copy from Host 2 Device : 0.000 Building kernels : 0.014 Allocation on Host for results : 0.000 Allocation on Device for results : 0.000 Synthesis of kernel : 0.006 Execution of kernel : 0.007 Copy from Device 2 Host : 0.000 OpenCLRate: 5123 Precision: 6.966685e-05 6.9132504e-05
Pour une sollicitation de la seconde GPU, la performance est moindre et c'est normal. La GPU Quadro K420 est très inférieure en performance à la GTX Titan.
Device Selection : 1 GpuStyle used : OpenCL Size of complex vector : 1024 Device #0 from NVIDIA Corporation of type xPU : NVIDIA GeForce GTX TITAN Device #1 from NVIDIA Corporation of type xPU : Quadro K420 Device #2 from The pocl project of type xPU : pthread-Intel(R) Xeon(R) CPU E5-2620 0 @ 2.00GHz Device #3 from Advanced Micro Devices, Inc. of type xPU : Intel(R) Xeon(R) CPU E5-2620 0 @ 2.00GHz Device #4 from Intel(R) Corporation of type xPU : Intel(R) Xeon(R) CPU E5-2620 0 @ 2.00GHz CPU/GPU selected: Quadro K420 Copy from Host 2 Device : 0.000 Building kernels : 0.566 Allocation on Host for results : 0.000 Allocation on Device for results : 0.000 Synthesis of kernel : 0.007 Execution of kernel : 0.019 Copy from Device 2 Host : 0.000 OpenCLRate: 1450 Precision: 6.966685e-05 6.9132504e-05
Maintenant, passons à la sélection du périphérique CUDA. Dans l'analuse de MetropolisCUDA de PiXPU.py, nous avons :
try:
# For PyCUDA import
import pycuda.driver as cuda
from pycuda.compiler import SourceModule
cuda.init()
for Id in range(cuda.Device.count()):
if Id==Device:
XPU=cuda.Device(Id)
print("GPU selected %s" % XPU.name())
print
except ImportError:
print("Platform does not seem to support CUDA")
Nous allons effectuer ces opérations sur MyDFT_8.py (copie de MyDFT7.py).
MyDFT_8.py- Libérez pour l'appel à la fonction
CUDADFT - Rajoutez le test exploitant la sélection OpenCL ou CUDA
- Modifiez l'appel de
CUDADFTpour intégrer le choix du périphérique - Modifiez la fonction
CUDADFTsur la base de la fonctionMetropolisCUDAdansPiXPU.py- supprimer l'import
pycuda.autoinit - rajouter la ligne
Context=XPU.make_context()après le parse des périphériques - rajouter la ligne
Context.pop()pour inactiver le contexte à la fin de la fonction - rajouter la ligne
Context.detach()ensuite
- Exécutez le programme avec l'option
-g CUDA - Exécutez le programme en sélectionnant la seconde GPU
Par défaut, la taille du vecteur complexe est 1024, le périphérique sollicité est 0 pour une utilisation en OpenCL. La sortie sur la machine ressemble à :
Device Selection : 0 GpuStyle used : CUDA Size of complex vector : 1024 Device #0 of type GPU : NVIDIA GeForce GTX TITAN Device #1 of type GPU : Quadro K420 GPU selected NVIDIA GeForce GTX TITAN Definition of kernel : 0.029 Synthesis of kernel : 0.000 Allocation on Host for results : 0.000 Execution of kernel : 0.044 CUDARate: 5262 Precision: 6.966685e-05 6.9132504e-05
Sur certaines configurations du CBP, une exécution en PyCUDA peut donner un message comparable au suivant :
Device Selection : 1
GpuStyle used : CUDA
Size of complex vector : 1024
Device #0 of type GPU : NVIDIA GeForce GTX TITAN
Device #1 of type GPU : Quadro K420
GPU selected Quadro K420
Traceback (most recent call last):
File "/home/equemene/bench4gpu/ETSN/./MyDFT_8.py", line 356, in <module>
k_np,l_np=CUDADFT(a_np,b_np,Device)
File "/home/equemene/bench4gpu/ETSN/./MyDFT_8.py", line 162, in CUDADFT
mod = SourceModule("""
File "/usr/lib/python3/dist-packages/pycuda/compiler.py", line 290, in __init__
cubin = compile(source, nvcc, options, keep, no_extern_c,
File "/usr/lib/python3/dist-packages/pycuda/compiler.py", line 254, in compile
return compile_plain(source, options, keep, nvcc, cache_dir, target)
File "/usr/lib/python3/dist-packages/pycuda/compiler.py", line 135, in compile_plain
raise CompileError("nvcc compilation of %s failed" % cu_file_path,
pycuda.driver.CompileError: nvcc compilation of /tmp/tmpccm0243v/kernel.cu failed
[command: nvcc --cubin -arch sm_30 -I/usr/lib/python3/dist-packages/pycuda/cuda kernel.cu]
[stderr:
nvcc fatal : Value 'sm_30' is not defined for option 'gpu-architecture'
]
-------------------------------------------------------------------
PyCUDA ERROR: The context stack was not empty upon module cleanup.
-------------------------------------------------------------------
A context was still active when the context stack was being
cleaned up. At this point in our execution, CUDA may already
have been deinitialized, so there is no way we can finish
cleanly. The program will be aborted now.
Use Context.pop() to avoid this problem.
-------------------------------------------------------------------
Aborted
En lisant attentivement, nous découvrons que le compilateur nvcc embarqué ne supporte pas la GPU Quadro K420 simplement parce qu'elle est trop vieille ! Ainsi, PyOpenCL montre là aussi sa supériorité : non seulement PyOpenCL permet une exécution sans modification sur CPU ou GPU, de manière plus efficace qu'avec Numpy ou Numba, mais en plus, sur GPU, elle offre moins de contraintes sur la distribution des tâches (pas de nécessité d'hybrider son programme en Blocks et Threads) et une pérennité dans le temps, que ce soit pour les GPU très anciennes ou très récentes !
Comme dernière modification sur notre , nous proposons de :
- lever l'inhibition des méthodes sous Python
- supprimer l'option
-g - rajouter une option à l'activation de la naive :
-n(défaut non) - rajouter une option à l'activation de la Numpy :
-y(défaut oui) - rajouter une option à l'activation de la Numba :
-a(défaut non) - rajouter une option à l'activation de la OpenCL :
-o(défaut oui) - rajouter une option à l'activation de la CUDA :
-c(défaut non) - rajouter une option au nombre de threads en CUDA :
-t(défaut 1024) - rajouter un test sur l'appel du noyau CUDA (cas threads non multiple de taille)
Nous trouverons ces modifications dans le programme MyDFT_9.py.
Exploration avec le "coeur" du GPU : xGEMM
Dans l'introduction sur les GPU, il était présenté la GPU comme un “gros” multiplicateur de matrices.
En effet, la méthode par shadering exploitait de nombreuses multiplications matricielles pour générer une image numérique (CGI ou Compute Generated Image). Il n'est donc pas étonnant que les GPU soient, historiquement, plutôt “efficaces” pour ce type de tâches : nous allons l'évaluer.
De BLAS aux xGEMM : les différentes implémentations
En calcul scientifique, l'objectif est de ne pas réinventer la roue à chaque modélisation numérique. Depuis presque 40 ans, la libraire d'algèbre linéaire la plus courante est la BLAS pour //Basic Linear Algebra Subprograms//.
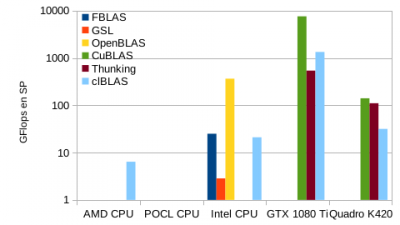
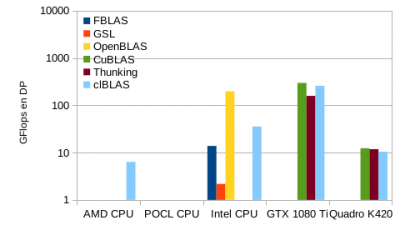
Ces routines peuvent être considérées comme des standards. De nombreuses implémentations existent pour toutes les architectures. Sur GPU, Nvidia propose sa propre version avec cuBLAS et AMD a placé en Open Source la sienne clBLAS.
Sur les CPU, Intel propose son implémentation largement optimisée pour ses processeurs au sein des librairies MKL mais les versions Open Sourcen notamment OpenBLAS, n'ont rien à leur envier. D'autres implémentations sont installées au CBP : l'ATLAS et la GSL.
Les librairies BLAS sont dans 3 catégories : celles manipulant exclusivement les vecteurs (1 dimension), celles manipulant les matrices et les vecteurs (1 et 2 dimensions), enfin celles manipulant exclusivement les matrices (2 dimensions).
L'implémentation de la multiplication de matrices dans les libairies BLAS est la xGEMM, avec x à remplacer par S, D, C et Z respectivement pour la Simple précision (32 bits), la Double précision (64 bits), la Complexe & simple précision et complexe & double précision (Z).
L'objectif de cette première manipulation est de commencer à comparer les GPU et les CPU avec cette opération simple.
Exploitations de xGEMM
Le dossier bench4gpu/BLAS/xGEMM contient peu de fichiers dont les importants sont : un unique programme source, xGEMM.c, et un fichier de construction, Makefile. C'est ce fichier qui va construire tous les exécutables d'un coup, à la fois pour les différentes implémentations de BLAS, mais aussi pour les deux précisions SP (simple précision sur 32 bits) et DP (double précision sur 64 bits).
Le source
Le programme source xGEMM.c a été conçu pour fonctionner avec n'importe quelle implémentation. Si vous l'éditez, vous réalisez qu'il n'est pas si simple d'avoir un programme qui s'exécute indifféremment quelle que soit la librairie. Même si les appels sont comparables (même nombre d'attributs dans les fonctions), leur nom change de librairie à librairie. Pour n'avoir qu'un seul source, les directives sont largement exploitées. C'est donc le Makefile qui va permettre de ne compiler que telle ou telle portion du programme source.
xGEMM.c et repérez les éléments suivants
- Identifiez dans
Makefilequelles directives (précédées par-D) sont associées aux différentes implémentations - Identifiez dans
xGEMM.cles “directives” C à base de#ifdefutilisées pour séparer les différentes implémentations - Repérez les deux implémentations FBLAS et OpenBLAS dans le programme à partir de l'analyse du
Makefile - Quelle différence existe-t-il dans les appels de la fonction
xGEMM? - Repérez les deux implémentations pour GPU Nvidia, les cublas et thunking
- Par quoi se distinguent les versions cublas et thunking ?*
Les exécutables
C'est simplement en lançant la commande make dans le dossier que la compilation s'opère. Ainsi, tous les exécutables commencent par xGEMM_SP_ ou xGEMM_DP_. Ils sont ensuite suffixés par l'implémentation BLAS :
Nous avons alors 12 exécutables de la forme xGEMM_SP_<version> ou xGEMM_DP_<version> :
openblasutilisant la librairie OpenBLAS, pour CPUgslutilisant la librairie GSL (pour GNU Scientific Librairies)fblasutilisant la librairie OpenBLAS mais pour des appels fortran, pour CPUcublasutilisant la librairie cuBLAS avec une gestion externe de la mémoirethunkingutilisant la librairie cuBLAS avec une gestion interne de la mémoireclblasutilisant la librairie clBLAS et OpenCL
Le programme appelé avec l'option -h donne quelques informations pour le lancement.
A l'exception de xGEMM_SP_clblas et xGEMM_DP_clblas, les paramètres d'entrée sont :
- la taille de la matrice
- le nombre d'itérations
Pour les programmes xGEMM_SP_clblas et xGEMM_DP_clblas, les paramètres d'entrée sont :
- la taille de la matrice
- le nombre d'itérations
- l'ID de la plateforme
- l'ID du périphérique
En appelant ces deux exécutables avec l'option -h, le programme détecte les plates-formes et périphériques.
La sortie offre comme informations :
- la durée moyenne d'exécution de chaque cycle
- l'estimation du nombre de GFlops
- l'erreur estimée par le calcul de la trace des matrices
Voici quelques exemples de lancement de ces exécutables sur une même machine, pour les CPU exclusivement :
$ ./xGEMM_SP_fblas 1000 10 Using FBLAS: 10 iterations for 1000x1000 matrix Duration of each cycle : 0.1597913000 s Number of GFlops : 25.020 Error 0.0000000000 $ ./xGEMM_SP_gsl 1000 10 Using GSL: 10 iterations for 1000x1000 matrix Duration of each cycle : 1.4037233000 s Number of GFlops : 2.848 Error 0.0000000000 $ ./xGEMM_SP_openblas 1000 10 Using CBLAS: 10 iterations for 1000x1000 matrix Duration of each cycle : 0.0109249000 s Number of GFlops : 365.953 Error 0.0000000000
Voici quelques exemples de lancement de ces exécutables sur une même machine, pour les GPU exclusivement :
$ ./xGEMM_SP_cublas 1000 10 Using CuBLAS: 10 iterations for 1000x1000 matrix Duration of memory allocation : 0.3678790000 s Duration of memory free : 0.0007630000 s Duration of each cycle : 0.0007413000 s Number of GFlops : 5393.228 Error 0.0000000000 $ ./xGEMM_SP_thunking 1000 10 Using CuBLAS/Thunking: 10 iterations for 1000x1000 matrix Duration of each cycle : 0.0447023000 s Number of GFlops : 89.436 Error 0.0000000000
Nous constatons d'abord une grosse disparité de performance. En analysant la durée d'un cycle, nous découvrons qu'il est inférieur à la milliseconde. Nous portons donc le nombre d'itérations à 1000, nous obtenons alors :
./xGEMM_SP_cublas 1000 1000 Using CuBLAS: 1000 iterations for 1000x1000 matrix Duration of memory allocation : 0.3984100000 s Duration of memory free : 0.0006670000 s Duration of each cycle : 0.0005262330 s Number of GFlops : 7597.395 Error 0.0000000000 root@opencluster2:/local/tests/bench4gpu/BLAS/xGEMM# ./xGEMM_SP_thunking 1000 1000 Using CuBLAS/Thunking: 1000 iterations for 1000x1000 matrix Duration of each cycle : 0.0073920040 s Number of GFlops : 540.855 Error 0.0000000000
Il faut donc prendre certaines précautions dans chaque évaluation de performances, notamment lorsque les durées d'exécution sont trop courtes.
Nous avons vu que plusieurs GPU peuvent coexister dans la machine. La question est de savoir lequel est sollicité lors d'un lancement de programme. Par défaut, avec les librairies CUDA, une seule GPU est sollicitée, souvent la première découverte. Pour savoir lequel a fait le travail, nous pouvons exploiter la commande nvidia-smi présentée ci-dessus pendant l'exécution du programme.
Dans le premier terminal qui nous sert à l'exécution des programmes, nous avons :
root@opencluster2:/local/tests/bench4gpu/BLAS/xGEMM# ./xGEMM_SP_cublas 1000 100000 Using CuBLAS: 100000 iterations for 1000x1000 matrix Duration of memory allocation : 0.3861840000 s Duration of memory free : 0.0007770000 s Duration of each cycle : 0.0005138863 s Number of GFlops : 7779.931 Error 0.0000000000
Dans le second terminal, dans lequel nous lançons des commandes de supervision, nous avons :
root@opencluster2:~# nvidia-smi
Sat Nov 24 12:10:59 2018
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 384.130 Driver Version: 384.130 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
|===============================+======================+======================|
| 0 GeForce GTX 108... Off | 00000000:3B:00.0 On | N/A |
| 27% 52C P2 254W / 250W | 248MiB / 11171MiB | 98% Default |
+-------------------------------+----------------------+----------------------+
| 1 Quadro K420 Off | 00000000:A1:00.0 Off | N/A |
| 25% 49C P8 N/A / N/A | 12MiB / 1999MiB | 0% Default |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: GPU Memory |
| GPU PID Type Process name Usage |
|=============================================================================|
| 0 6477 C ./xGEMM_SP_cublas 199MiB |
| 0 6681 G /usr/lib/xorg/Xorg 36MiB |
+-----------------------------------------------------------------------------+
Nous voyons que le GPU #0, identifié comme la GTX 1080 Ti, exécute 2 tâches : /usr/lib/xorg/Xorg et ./xGEMM_SP_cublas. Nous avons également l'empreinte mémoire de chacun des processus : 36MiB pour le Xorg et 199MiB pour notre programme xGEMM_SP_cublas.
La question légitime est de se demander, dans le cas d'une machine multi-gpu, comment “contrôler” sur quele GPU est exécutée le programme. Il existe des méthodes assez comparables à celles de OpenCL pour la découverte des périphériques, mais elles sont généralement peu exploitées dans les programmes. La technique la plus classique reste l'utilisation d'une variable d'environnement, laquelle va “contraindre” l'exploitation d'un (ou plusieurs) GPU(s) : CUDA_VISIBLE_DEVICES.
Par exemple, si nous précisons que cette variable vaut 1, le périphérique Nvidia #1 sera le seul sollicité. Ainsi, en lançant la commande préfixée de cette variable valuée, nous avons :
$ CUDA_VISIBLE_DEVICES=1 ./xGEMM_SP_cublas 1000 1000 Using CuBLAS: 1000 iterations for 1000x1000 matrix Duration of memory allocation : 0.1777080000 s Duration of memory free : 0.0005750000 s Duration of each cycle : 0.0283741830 s Number of GFlops : 140.903 Error 0.0000000000
Et pendant l'exécution, dans la fenêtre de commandes de supervision :
root@opencluster2:~# nvidia-smi
Sat Nov 24 12:21:26 2018
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 384.130 Driver Version: 384.130 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
|===============================+======================+======================|
| 0 GeForce GTX 108... Off | 00000000:3B:00.0 On | N/A |
| 24% 37C P8 12W / 250W | 39MiB / 11171MiB | 0% Default |
+-------------------------------+----------------------+----------------------+
| 1 Quadro K420 Off | 00000000:A1:00.0 Off | N/A |
| 30% 59C P0 N/A / N/A | 51MiB / 1999MiB | 100% Default |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: GPU Memory |
| GPU PID Type Process name Usage |
|=============================================================================|
| 0 6681 G /usr/lib/xorg/Xorg 36MiB |
| 1 8192 C ./xGEMM_SP_cublas 39MiB |
+-----------------------------------------------------------------------------+
Nous pouvons évidemment appliquer la même approche du préfixe avec l'autre implémentation CUDA (le mode Thunking) :
$ CUDA_VISIBLE_DEVICES=1 ./xGEMM_SP_thunking 1000 1000 Using CuBLAS/Thunking: 1000 iterations for 1000x1000 matrix Duration of each cycle : 0.0361565210 s Number of GFlops : 110.575 Error 0.0000000000
Avec les implémentations OpenCL, il est possible, sans variable, de s'adresser avec un unique exécutable, à chacun des périphériques (CPU ou GPU) quelle que soit leur implémentation :
$ ./xGEMM_SP_clblas 1000 10 0 0 Using CLBLAS: 10 iterations for 1000x1000 matrix on (0,0) Device (0,0): Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz Duration of memory allocation : 0.2068470000 s Duration of memory free : 0.0105010000 s Duration of each cycle : 0.6236489000 s Number of GFlops : 6.411 Error 0.0000000000 $ ./xGEMM_SP_clblas 1000 10 1 0 Using CLBLAS: 10 iterations for 1000x1000 matrix on (1,0) Device (1,0): pthread-Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz 1 warning generated. 1 warning generated. 1 warning generated. 1 warning generated. 1 warning generated. 1 warning generated. 1 warning generated. 1 warning generated. ./xGEMM_SP_clblas: symbol lookup error: /root/.cache/pocl/kcache/DO/MOINFKPIFEHKLMFJBAMOHIHHPGDFMKFNMCFAG/sgemm_Col_NN_B0_MX032_NX032_KX08/16-16-1/sgemm_Col_NN_B0_MX032_NX032_KX08.so: undefined symbol: mem_fence root@opencluster2:/local/tests/bench4gpu/BLAS/xGEMM# ./xGEMM_SP_clblas 1000 10 1 0 Using CLBLAS: 10 iterations for 1000x1000 matrix on (1,0) Device (1,0): pthread-Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz ./xGEMM_SP_clblas: symbol lookup error: /root/.cache/pocl/kcache/DO/MOINFKPIFEHKLMFJBAMOHIHHPGDFMKFNMCFAG/sgemm_Col_NN_B0_MX032_NX032_KX08/16-16-1/sgemm_Col_NN_B0_MX032_NX032_KX08.so: undefined symbol: mem_fence $ ./xGEMM_SP_clblas 1000 1000 2 0 Using CLBLAS: 1000 iterations for 1000x1000 matrix on (2,0) Device (2,0): GeForce GTX 1080 Ti Duration of memory allocation : 0.3912880000 s Duration of memory free : 0.0025020000 s Duration of each cycle : 0.0029808910 s Number of GFlops : 1341.210 Error 0.0000000000 $ ./xGEMM_SP_clblas 1000 1000 2 1 Using CLBLAS: 1000 iterations for 1000x1000 matrix on (2,1) Device (2,1): Quadro K420 Duration of memory allocation : 0.2507630000 s Duration of memory free : 0.0019840000 s Duration of each cycle : 0.1263268040 s Number of GFlops : 31.648 Error 0.0000000000 $ ./xGEMM_SP_clblas 1000 1000 3 0 Using CLBLAS: 10 iterations for 1000x1000 matrix on (3,0) Device (3,0): Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz Duration of memory allocation : 0.2919330000 s Duration of memory free : 0.0030360000 s Duration of each cycle : 0.1896384000 s Number of GFlops : 21.082 Error 0.0000000000
Nous pouvons également constater que certains périphériques ne “passent” pas en OpenCL et que les performances sont très variables.
Voici un synoptique des performances pour les différentes implémentations et les différents GPU en simple précision. Les performances ont été placées en log. Les GPU présentent des performances incroyablement supérieures au processeur (autour d'un facteur 20 pour la GTX 1080 Ti face à la meilleure des implémentations pour CPU).
Lors du passage en double précision, les GPU se rapprochent des CPU en performance.
Le ratio entre performances en simple sur double précision illustre la grosse différence entre CPU et GPU.
xGEMM_<precision>_<implementation> avec une taille de 1000
- Variez le nombre d'itérations pour obtenir une durée d'exécution d'une dizaine de secondes ?
- Laquelle des implémentations CPU est la plus performante ?
- Laquelle des implémentations GPU est la plus performante ?
- Exécutez à nouveau la performance en passant la précision (de SP à DP) sur CPU
- Evaluez le rapport de performances entre SP et DP sur CPU
- Exécutez à nouveau la performance en passant la précision (de SP à DP) sur GPU
- Evaluez le rapport de performances entre SP et DP sur GPU
- Présentez les performances entre implémentations en simple précision
- Présentez les performances entre implémentations en double précision
Il est aussi intéressant de constater que la performance dépend non seulement de l'implémentation, du périphérique mais aussi de sa sollicitation. Voici la performance pour l'implémentation CPU avec OpenBLAS et les implémentations cuBLAS et Thunking sur la GTX 1080 Ti.
- Diminuez la taille aux valeurs suivantes
125,250,500et exécutez les programmes - Que constatez-vous pour les performances sur CPU ou GPU ?
- Augmentez la taille à
2000,4000,8000,16000et exécutez les programmes - Que constatez-vous pour les performances sur CPU ou GPU ?
- Pendant une exécution, observez la consommation électrique instantanée : que constatez-vous ?
- Présentez les performances en fonction des tailles explorées
Exploration de "codes métiers"
Introduction à l'intégration de codes
Les “codes métiers” sont des programmes “de production scientifique”. Il n'est pas question, pour un utilisateur, de modifier le source du programme pour ses activités, notamment de recherche. Le programme est exploité “tel quel” et seuls les paramètres d'entrées changent.
Par contre l'intégration d'un code dans un environnement informatique (tuple matériel, système d'exploitation, librairies, logiciel, usage) peut s'avérer compliqué, voire complexe. Cette activité d'intégration forme une grande partie de l'activité des personnels des infrastructures de calcul scientifique.
Exploitation en Deep Learning avec TensorFlow
Nous allons tenter d'exploiter un des exemples présentés dans les tutoriels de TensorFlow.
L'exploitation des GPU a littéralement “explosé” lorsque le Machine Learning ou le Deep Learning sont devenus des modes. En effet, la puissance “brute” des GPU peut enfin être exploitée sans trop de portage, notamment par l'exploitation des librairies BLAS ou cuDNN.
L'exemple sur lequel nous allons nous pencher est le DeepCNN.
L'intégration de TensorFlow avec une exploitation des GPU est plutôt ardue à partir des sources, étant donné le nombre de dépendances. L'approche Conda permet d'installer un “environnement système” bâti essentiellement autour d'applications Python. Conda permet également à tout utilisateur de créer son propre environnement complet lui permettant un suivi personnel de ses outils.
Au CBP, un environnement Conda a été installé pour permettre l'exploitation de la majorité des outils construits autour de TensorFlow. Le chargement de l'environnement se réalise en “sourçant” l'environnement CONDA avec la commande suivante :
module load conda3/4.9.2
La commande précédente “paramètre” les variables d'environnement nécessaires l'exploitation de l'environnement complet CONDA installé pour vous dans /opt/conda3-4.9.2/
L'objectif est de “jouer” le tutoriel exploitant la base d'images CIFAR10 pour un apprentissage convolutif.
- chargez l'environnement conda
- préparez la variable d'environnement
TIME - ouvrez un terminal et tapez
dstatpour monitorer le système - ouvrez un terminal et tapez
nvidia-smi dmonpour la GPU - lancez un
ipythondans un terminal - appliquez ligne à ligne le tutoriel et regardez l'activité réseau
- vérifiez que vous obtenez des résultats comparables
- récupérez dans un fichier
CIFAR10.pytoutes les commandes du tutoriel - inhiber les lignes associées à un affichage (préfixées par
plt - lancez le fichier préfixé de
/usr/bin/time python - notez le temps écoulé (
TIME Elapsed) pour cette première exécution - relancez le fichier préfixé de
/usr/bin/time python - notez le temps écoulé (
TIME Elapsed) pour cette seconde exécution - inhibez les GPU Nvidia avec
CUDA_VISIBLE_DEVICES - relancez le fichier préfixé de
/usr/bin/time python - vérifiez que la GPU est inutilisée
- notez le temps écoulé (
TIME Elapsed) pour cette troisième exécution - comparez les temps d'exécution et sur l'efficacité d'usage de la GPU
En regardant l'activité du GPU, il apparaît que le gain est substanciel par rapport à une “petite” configuration GPU. Cependant, la nature du réseau créé n'exploitait pas de manière optimale la GPU par rapport à la CPU. Une petite modification de notre réseau va permettre de mettre cela en évidence, en modifiant le nombre de poids d'une des couches neuronales.
- changez 64 en 65536 dans
model.add(layers.Dense(64, activation='relu')) - supprimez la référence à
CUDA_VISIBLE_DEVICESavecexport -n CUDA_VISIBLE_DEVICES - relancez l'apprentissage
/usr/bin/time python CIFAR10.py - notez dès le début d'un cycle l'ETA (Estimate Time of Arrival)
- contrôlez l'activité de la GPU
- arrêtez l'apprentissage avec un <Ctrl><C>
- inhibez la GPU
- relancez l'apprentissage
/usr/bin/time python CIFAR10.py - notez dès le début d'un cycle l'ETA
- arrêtez l'apprentissage avec un <Ctrl><C>
- effectuez le rapport entre les ETA
Sur la machine k40 équipée d'une GPU Tesla K40 ancienne et de deux CPU E5-2609v2, le ratio est de 15. Le plus intéressant vient de la comparaison avec la machine au CBP disposant des processeurs les plus performants : 2 AMD Epyc 7742 avec chacun 64 coeurs. Ces derniers sont 3x moins rapides que la K40 sur cette opération. Ainsi, même de vieilles GPU (génération N-5) peuvent encore, dans des opérations de Machine Learning, s'avérer efficaces, dès lors que les problèmes sont correctement dimensionnés pour elles.
Intégration et exploitation du code GENESIS
Le code GENESIS de l'institut RIKEN Center for Computational Science est un logiciel de dynamique moléculaire. Présenté comme exploitant massivement les GPU, il est disponible sur bitbucket. C'est un programme hybride (exploitant 2 stratégies de parallélisation), et même trhybride dans la mesure où il exploite les GPU de type Nvidia avec CUDA, la distribution sur les coeurs via OpenMP et la distribution sur des noeuds différents via passage de messages MPI. Le code source est accessible à l'adresse : https://www.r-ccs.riken.jp/labs/cbrt/download/genesis-version-1-5/
- Lisez la documentation d'installation
- Placez les sources dans le dossier
/local/$USER/GENESIScréé pour l'occasion - Préparez une compilation pour GPU en simple précision dans le dossier
/local/$USER/GENESIS/gpu-single - Compilez et installez le programme
- Purgez la compilation précédente
- Préparez une compilation pour CPU en simple précision dans le dossier
/local/$USER/GENESIS/cpu-single - Compilez et installez le programme
L'exécution du programme est évaluée en comparant son exécution dans différentes configurations d'exploitation des CPU et des GPU.
Pour cela, l'exemple de la base de tests de régression. Le test test_rpath_spdyn/alad_water a été modifié pour durer un peu plus longtemps à l'exécution.
De plus, GENESIS étant trhybride, il est programmé pour se distribuer sur des machines indépendantes qui communiquent par échanges de messages. Le test ''alad_water'' exige, par construction de la simulation, quatre exécutions concurrentes lesquelles vont communiquer par MPI. Il faudra donc préfixer l'exécutable de mpirun -np 4 pour exécuter ces quatre tâches.
De plus, ce programme est aussi parallélisé avec OpenMP : il va donc “aussi” exploiter les coeurs disponibles. Le souci, c'est que, par défaut, il va lancer pour chaque tâche MPI autant de sous-tâches OpenMP que de coeurs (même “virtuels”) disponibles sur la machine. Ainsi, en exécutant l'exemple alad_water sur une machine disposant de 8 coeurs Hyperthreadés (donc disposant au total de 16 coeurs logiques), il va lancer 4*16 soit 64 tâches pour seulement 8 “vrais” coeurs : de quoi surcharger la machine.
Pour finir, dans comme ce programme est “aussi” gépufié (porté sur GPU), il risque d'y avoir un goulet d'étranglement pour l'accès au GPU pour les 64 tâches simultanées. Ainsi, les programmes “fortement” parallélisés exigent de choisir judicieusement les différents paramètres de parallélisation tout comme nous avons vue que, pour les GPU, il fallait découper la tâche en un nombre optimal de sous-tâches.
alad_water- Récupérez l'exemple d'exécution
- Décompressez l'archive dans
/local/$USER/GENESIS - Exécutez le programme sur l'exemple avec la version CPU
/usr/bin/time mpirun -np 4 /local/$USER/GENESIS/cpu-single/bin/spdyn inp
- Observez pendant l'exécution l'activité des coeurs
- Notez le
Elapsed Timeet leSystem Time - Effacez les résultats
test*avecrm test* - Exécutez le programme sur l'exemple avec la version GPU
- Exécutez la commande
/usr/bin/time mpirun -np 4 /local/$USER/GENESIS/gpu-single/bin/spdyn inp
- Observez pendant l'exécution l'activité des coeurs et des GPU
- Notez le
Elapsed Timeet leSystem Time - Effacez les résultats
test*avecrm test* - Déterminez, sachant que 4 tâches MPI simultanément, combien de threads lancer
- Définissez ce nombre pour le système avec la fonction suivante :
export OPTIMAL_THREADS=<MonCHoixJudicieux>
- Exécutez la commande
/usr/bin/time mpirun -np 4 -x OMP_NUM_THREADS=$OPTIMAL_THREADS /local/$USER/GENESIS/cpu-single/bin/spdyn inp - Notez le
Elapsed Timeet leSystem Time - Effacez les résultats
test*avecrm test* - Exécutez la commande
/usr/bin/time mpirun -np 4 -x OMP_NUM_THREADS=$OPTIMAL_THREADS /local/$USER/GENESIS/gpu-single/bin/spdyn inp - Notez le
Elapsed Timeet leSystem Time - Concluez sur la pertinence de l'utilisation de l'option
-x OMP_NUM_THREADS=$OPTIMAL_THREADS
Intégration et exploitation du code Gromacs
Nous allons tenter de reproduire une expérience de Nvidia vantant l'efficacité des GPGPU pour le logiciel de dynamique moléculaire Gromacs.
- La documentation offre ceci :
- récupérez le source
- étendez l'archive
- créez un dossier pour la construction
- passez dans ce dossier
- préparez la compilation
- compilez le code
- installez les exécutables
- A quelle étape est-ce que cela bloque ? Quel message avez-vous ?
- Trouvez une méthode permettant de régler ce problème.
En cas de difficultés, appliquez la recette de Gromacs pour Debian Buster ![]()
1536- Quel
Elapsed Timeavez-vous pour l'exécution sur GPU (et CPU) ? - Quel
Elapsed Timeavez-vous pour l'exécution uniquement sur CPU ? - Quel ratio de performances existe entre les deux exécutions ?
Exploration des GPU avec un Pi Monte Carlo
Le "Pi Monte Carlo" ou "Pi Dart Dash",un code "compute bound"
Le calcul de Pi par la méthode de Monte Carlo est exemplaire à plusieurs titres :
- elle est simple : un générateur de nombres aléatoires, un mécanisme de test et un compteur suffisent
- elle est parallélisable : en distribuant le nombre d'itérations sur les unités de calcul
- elle est compute bound : en n'ayant quasiment aucun accès mémoire (reste dans les registres de calcul)
- elle est cependant notoirement inefficace pour calculer Pi

Les versions que vous allez utiliser exploitent de 2 à 4 paramètres en entrée :
- le nombre total d’itérations
- le régime de Parallélisme (PR) : le découpage du travail vers les unités de traitement
- le type de variables : INT32, INT64, FP32, FP64
- le type de Random Number Generator : MWC, CONG, SHR3, KISS
Intuitivement, le régime de parallélisme à explorer est optimal lorsqu'il correspond au nombre d'unités de traitement (Compute Units). Nous verrons que c'est un peu plus compliqué que cela.
Le type de variable va permettre de juger de l'efficacité des Compute Units en fonction des données qu'elles manipulent, notamment lorsque nous passons de 32 à 64 bits.
Le type de RNG a aussi son importance. Les RNG utilisés ici sont ceux de Georges Marsaglia. Comme tous les RNG pseudo-aléatoires, ils nécessitent une “graine”, laquelle permet une reproductibilité des tirages. Voici leur code source, d'une effroyable efficacité compte-tenu de leur compacité.
#define znew ((z=36969*(z&65535)+(z>>16))<<16) #define wnew ((w=18000*(w&65535)+(w>>16))&65535) #define MWC (znew+wnew) #define SHR3 (jsr=(jsr=(jsr=jsr^(jsr<<17))^(jsr>>13))^(jsr<<5)) #define CONG (jcong=69069*jcong+1234567) #define KISS ((MWC^CONG)+SHR3)
Comme nous divisons un nombre d'itérations entier par un régime de parallélisme, nous approximons dans le code le nombre d'itérations de chaque calcul élémentaire à l'entier supérieur. Lorsque le nombre d'itérations dépasse le milliard, le nombre d'itérations supplémentaires ne dépasse pas 7%.
Comme résultat, nous avons deux observables simples :
- une estimation de Pi : juste indicative, Pi n'étant pas rationnel
- par l'addition de tous les résultats sur le nombre total d'itérations que multiplie 4
- le temps écoulé
Pour évaluer une performance, il est toujours intéressant de choisir une métrique maximaliste : nous définissons le itops soit le ITerative Operations Per Second comme le rapport entre ce nombre total d'itérations et le temps écoulé.
Les programmes utilisés : OpenCL, CUDA
Le dossier bench4gpu contient de nombreuses implémentations de ce calcul élémentaire. Nous nous focaliserons sur 2 d'entre eux :
bench4gpu/Pi/OpenCL/PiOpenCL.cbench4gpu/Pi/XPU/PiXPU.py
Implémentation C/OpenCL
Le programme bench4gpu/Pi/C/OpenCL/PiOpenCL.c est une implémentation en C “pur” : il permet de juger de la difficulté d'appropriation de OpenCL. En effet, une grande partie du code est destinée à définir quelle plateforme et quel périphérique utiliser, placer les données à traîter.
- Repérez dans le programme source le noyau OpenCL réalisant le calcul
- Repérez dans le programme source les parties découverte des périphériques
- Repérez quel RNG est utilisé dans ce programme
Le code se compile très simplement uniquement en appliquant la commande gcc -o PiOpenCL PiOpenCL.c -lOpenCL -lm. L'exécutable PiOpenCL est prêt à être utilisé.
Son exécution sans paramètre ne fait qu'une “découverte” des périphériques OpenCL disponibles et présente la documentation. Par exemple :
Performs a Pi estimation by Dart Dash: #1 OpenCL Plateform ID (default 0) #2 OpenCL Device ID (default 0) #3 Minimal number of iterations (default 1000000) #4 Parallel Rate (default 1024) #5 Loops (default 1) #6 Type of variable: INT32, INT64, FP32, FP64 (default FP32) OpenCL statistics: 4 platform(s) detected Device (0,0): Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz Device Type: CL_DEVICE_TYPE_CPU Device vendor: GenuineIntel Hardware version: OpenCL 1.2 AMD-APP (1912.5) Software version: 1912.5 (sse2,avx) OpenCL C version: OpenCL C 1.2 Parallel compute units: 16 Maximum Work Group Size: -697485824 Maximum Work Item Sizes: 0 Device (1,0): pthread-Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz Device Type: CL_DEVICE_TYPE_CPU CL_DEVICE_TYPE_DEFAULT Device vendor: GenuineIntel Hardware version: OpenCL 2.0 pocl Software version: 0.13 OpenCL C version: OpenCL C 2.0 Parallel compute units: 16 Maximum Work Group Size: -697485824 Maximum Work Item Sizes: 0 Device (2,0): GeForce GTX 1080 Ti Device Type: CL_DEVICE_TYPE_GPU Device vendor: NVIDIA Corporation Hardware version: OpenCL 1.2 CUDA Software version: 384.130 OpenCL C version: OpenCL C 1.2 Parallel compute units: 28 Maximum Work Group Size: -697485824 Maximum Work Item Sizes: 0 Device (2,1): Quadro K420 Device Type: CL_DEVICE_TYPE_GPU Device vendor: NVIDIA Corporation Hardware version: OpenCL 1.2 CUDA Software version: 384.130 OpenCL C version: OpenCL C 1.2 Parallel compute units: 1 Maximum Work Group Size: -697485824 Maximum Work Item Sizes: 0 Device (3,0): Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz Device Type: CL_DEVICE_TYPE_CPU Device vendor: Intel(R) Corporation Hardware version: OpenCL 2.0 (Build 25) Software version: 1.2.0.25 OpenCL C version: OpenCL C 2.0 Parallel compute units: 16 Maximum Work Group Size: -697485824 Maximum Work Item Sizes: 0
Nous découvrons que 4 plates-formes sont détectées, servant 5 périphériques.
- les 3 implémentations CPU de OpenCL : celles d'AMD, de PortableCL et d'Intel
- les 2 GPU Nvidia GTX 1080 Ti et Quadro K420
Cette sortie montre également les options (au moins 2) à entrer pour exploiter le programme :
- #1 l'identifiant de la plateforme
- #2 l'identifiant du périphérique pour cette plateforme
- #3 le nombre minimum d'itérations (par défaut 1000000)
- #4 le régime de parallélisme PR (par défault 1024)
- #5 le nombre de boucles (par défault 1) : bien utile pour évaluer la reproductibilité temporelle
- #6 le type de variable: INT32, INT64, FP32, FP64 (par défault FP32)
Il est donc nécessaire de préciser uniquement le tuple (plateforme,périphérique) pour exécuter le programme.
- Compilez le programme avec la ligne de compilation précisée ci-dessus
- Exécutez le programme “à vide” et identifiez les périphériques
- Exécutez le programme sur la première GPU Nvidia que vous avez repérée
Avec ce premier outil, il est possible de juger de la différence fondamentale de performances entre GPU et CPU, en fonction du régime de parallélisme.
Par exemple, sur les périphériques ci-dessus :
| Périphérique | Durée | Itops | Inside |
|---|---|---|---|
| AMD | 3.98 | 251524870 | 785423827 |
| PortableCL | 4.77 | 209512671 | 785423827 |
| GTX 1080 Ti | 26.11 | 38299749 | 785423825 |
| Quadro K420 | 108.52 | 9214573 | 785423825 |
| Intel | 3.90 | 256424327 | 785423825 |
Il est assez intéressant que les implémentations CPU offrent quasiment la même performance. Par contre les GPU offrent une performance bien moindre (6x moins pour la GTX 1080 Ti et presque 30x moins pour la Quadro K420).
Il est aussi intéressant qu'étrange que le nombre de “coups” à l'intérieur du quadrant d'exploration ne soit pas le même pour toutes les implémentations. C'est un artéfact lié à la multiplication du RNG par la constante pour le placer entre 0 et 1.
- Exécutez le programme sur toutes (GPU & CPU) avec un nombre d'itérations de 1 milliard
- Repérez les éléments de durée, itops et le inside
- Tracez l'histogramme correspondant aux performances sur le modèle ci-dessus
- Quel ratio existe entre le ou les GPU et les processeurs ?
Nous pouvons maintenant explorer la réponse des périphériques, notamment pour des régimes de parallélisme bien plus élevés, par exemple la valeur par défaut de 1024. Nous portons par contre le nombre d'itérations à 10000000000, soit 10x plus que précédemment.
| Périphérique | Durée | Itops | Inside |
|---|---|---|---|
| AMD | 4.28 | 2338471813 | 7853958701 |
| PortableCL | 24.23 | 412737304 | 7853958701 |
| GTX 1080 Ti | 0.37 | 26864605077 | 7853958630 |
| Quadro K420 | 3.04 | 3287218047 | 7853958630 |
| Intel | 1.25 | 7973063801 | 7853958630 |
Cette seconde expérience montre de manière assez spectaculaire que les GPU ne dévoilent leur puissance “que” pour des régimes de parallélisme élevé. Notons aussi que les implémentations sur CPU ont des performances très très disparates.
- Exécutez le programme sur toutes (GPU & CPU) avec un nombre d'itérations de 10 milliards
- Repérez les éléments de durée, itops et inside
- Tracez l'histogramme correspondant aux performances sur le modèle ci-dessus
- Quel ratio existe entre le ou les GPU et les processeurs ?
Dans l'expérience précédente, nous avons exploité un régime de parallélisme sur les processeurs très supérieur au nombre de Compute Units, lesquelles sont identifiées comme les coeurs. Il y avait 8 coeurs physiques et nous avons “chargé” chaque coeur à 256 fois leur charge. Que se passe-t-il si nous effectuons la même chose avec les GPU ?
Dans notre exemple, la GTX 1080 Ti dispose de 3584 cuda cores. La Quadro K420 de 192 cuda cores. Explorons ces périphériques avec des PR de 256x ces valeurs (nous sommes obligés de porter les itérations à 1000 milliards) :
| Périphérique | Durée | Itops | Inside |
|---|---|---|---|
| GTX 1080 Ti | 3.77 | 265583420021 | 785397498152 |
| Quadro K420 | 290.03 | 3447937882 | 785398065372 |
Ce graphique montre sans ambiguité la puissance “brute” qu'offre une GPU de gamer en comparaison de CPU traditionnelle (33x dans la meilleure implémentation CPU, celle d'Intel). Notons également que GPU n'est pas synonyme de puissance brute : la “petite” Quadro K420, bien que “professionnelle” présente des performances 77x inférieures.
- Reprenez les spécifications des GPU et isolez le nombre de cuda cores
- Exécutez le programme sur les GPU avec un nombre d'itérations de 100 milliards et un PR de 256x le nombre de cuda cores
- Repérez les éléments de durée, itops et inside
- Tracez l'histogramme correspondant aux performances sur le modèle ci-dessus
- Quel ratio de performance existe entre la GPU la plus puissante et la meilleure implémentation des CPU ?
Nous avons déjà noté, dans l'exploitation de xGEMM que les performances pour les GPU étaient largement influencées par la précision utilisée pour les calculs.
Pour les mêmes périphériques mais en passant en double précision, nous avons :
| Périphérique | Elapsed | Itops | Inside |
|---|---|---|---|
| AMD | 4.05 | 2472082769 | 7853958184 |
| PortableCL | 18.89 | 529471467 | 7853958184 |
| GTX 1080 Ti | 3.34 | 29909278511 | 78540290903 |
| QuadroK420 | 12.52 | 798857983 | 7854068741 |
| Intel | 16.24 | 6156907937 | 78539995659 |
Nous avons présenté dans le cours qu'un mauvais choix de régime de parallélisme pouvait largement influencer la performance.
Par exemple, regardons pour la meilleure implémentation de CPU et pour la GPU la plus puissante, quelle influence a le choix du régime de parallélisme autour du régime de parallélisme optimal.
- Reprenez les expériences ci-dessus en précisant un calcul en double précision
- Tracez l'histogramme avec tous les périphériques OpenCL
- Quel ratio de performance existe entre la GPU la plus puissante et la meilleure implémentation des CPU ?
Implémentation Python/OpenCL Python/CUDA
Dans l'exemple précédent, nous avons exploité un programme en C “pur”. Nous avons vu comment s'intégrait la portion de code (le noyau ou le kernel) qui était exécutée, soit par les GPU, soit par différentes implémentations pour CPU de OpenCL. Nous avons aussi pu “juger” du côté assez “compliqué” de découvertes des périphériques et des mécanismes d'entrée/sortie.
Avec le programme PiXPU.py, situé dans le dossier bench4gpu/Pi/XPU nous allons pouvoir exploiter les périphériques de calcul plus simplement, et bénéficier de toutes les facilités d'un langage évolué.
Regardons d'abord sa sortie lorsqu'il est sollicité avec l'option -h :
$ cd $HOME/bench4gpu/Pi/XPU $ python3 PiXPU.py -h PiXPU.py -o (Out of Core Metrology) -c (Print Curves) -k (Case On IfThen) -d <DeviceId> -g <CUDA/OpenCL> -i <Iterations> -b <BlocksBegin> -e <BlocksEnd> -s <BlocksStep> -f <ThreadsFirst> -l <ThreadsLast> -t <ThreadssTep> -r <RedoToImproveStats> -m <SHR3/CONG/MWC/KISS> -v <INT32/INT64/FP32/FP64> Informations about devices detected under OpenCL API: Device #0 from Advanced Micro Devices, Inc. of type xPU : Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz Device #1 from The pocl project of type xPU : pthread-Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz Device #2 from NVIDIA Corporation of type xPU : GeForce GTX 1080 Ti Device #3 from NVIDIA Corporation of type xPU : Quadro K420 Device #4 from Intel(R) Corporation of type xPU : Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz Informations about devices detected under CUDA API: Device #0 of type GPU : GeForce GTX 1080 Ti Device #1 of type GPU : Quadro K420
Nous disposons de plus d'options pour le lancement. Ce programme étant un programme de test de performances, il permet une exploration de régimes de parallélisme. Dans les approches de programmation CUDA ou OpenCL, il y a deux étages de parallélisme :
- le premier pour des tâches indépendantes : Blocks et Work items en sont les éléments
- le second pour des tâches nécessitant une synchronisation : ce sont les Threads
Il y a donc, pour explorer ces deux régimes de parallélisme, 6 options différentes :
-b <BlocksBegin>: le premier nombre de Work items ou de Blocks à explorer-e <BlocksEnd>: le dernier nombre de Work items ou de Blocks à explorer-s <BlocksStep>: le pas entre deux Work items ou de Blocks-f <ThreadsFirst>: le premier nombre de Threads à explorer-l <ThreadsLast>: le dernier nombre de Threads à explorer-t <ThreadssTep>: le pas entre deux Threads à explorer
Il est aussi possible de coupler les deux régimes de parallélisme en appelant 16 work items avec 16 threads.
Par exemple, pour explorer des régimes de parallélisme de 16 à 128 avec des pas de 16 en Work items et 4 à 8 en Threads avec des pas unitaires, nous aurons -b 16 -e 128 -s 16 -f 4 -l 8 -t 1 -p 2.
D'autres options :
-g <CUDA/OpenCL>: pour sélectionner l'utilisation de CUDA ou OpenCL-i <Iterations>: pour le nombre total d'itérations-r <RedoToImproveStats>: pour refaire plusieurs expériences en série-m <SHR3/CONG/MWC/KISS>: pour sélectionner le type de Random Number Generator de Marsaglia-v <INT32/INT64/FP32/FP64>: pour sélectionner le type de variable à exploiter-k (Case On IfThen): pour forcer l'exploitation du test avec un mécanisme enIfThen-d <DeviceId>: pour sélectionner le périphérique en utilisant l'ID fourni avec le-h
L'appel du programme ci-dessus nous montre qu'il y a le même nombre de périphériques OpenCL visibles (les 3 implémentations OpenCL pour CPU et les 2 GPU Nvidia), la nouveauté est que nous voyons également deux périphériques CUDA.
En sortie, lors d'un appel simple ne précisant que le périphérique, ici le premier, #0, nous avons :
$ python3 PiXPU.py -d 0
Devices Identification : [0]
GpuStyle used : OpenCL
Iterations : 10000000
Number of Blocks on begin : 1
Number of Blocks on end : 1
Step on Blocks : 1
Number of Threads on begin : 1
Number of Threads on end : 1
Step on Threads : 1
Number of redo : 1
Metrology done out of XPU : False
Type of Marsaglia RNG used : MWC
Type of variable : FP32
Device #0 from Advanced Micro Devices, Inc. of type xPU : Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz
Device #1 from The pocl project of type xPU : pthread-Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz
Device #2 from NVIDIA Corporation of type xPU : GeForce GTX 1080 Ti
Device #3 from NVIDIA Corporation of type xPU : Quadro K420
Device #4 from Intel(R) Corporation of type xPU : Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz
([0], {0: 'xPU'})
('Inside ', {'Blocks': 1, 'ValueType': 'FP32', 'RNG': 'MWC', 'Threads': 1, 'Iterations': 10000000, 'Device': 0, 'Steps': 1, 'IfThen': False})
('CPU/GPU selected: ', 'Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz')
(Blocks/Threads)=(1,1) method done in 0.06 s...
{'Duration': array([0.06270599]), 'Inside': 7852019.0, 'NewIterations': 10000000}
Pi estimation 3.14080760
0.06 0.06 0.00 0.06 0.06 159474388 159474388 0 159474388 159474388
Deux fichiers de sortie sont créés et reprennent dans leur titre les paramètres d'entrée :
Pi_FP32_MWC_xPU_OpenCL_1_1_1_1_10000000_Device0_InMetro_opencluster2Pi_FP32_MWC_xPU_OpenCL_1_1_1_1_10000000_Device0_InMetro_opencluster2.npz
Le premier est uniquement lisible avec Python, le second est utilisable directement, pas exemple avec GNUplot.
Examen du code source
- Editez le code source avec l'outil
gedit - Identifiez l'appel de la procédure principale OpenCL : ligne
- Identifiez la zone de code de cette procédure OpenCL : lignes
- Examinez dans cette procédure la construction du noyau OpenCL : ligne
- Examinez dans cette procédure l'appel du noyau OpenCL : ligne
- Identifiez le noyau OpenCL appelé par cette procédure : lignes
- Identifiez l'appel de la procédure principale CUDA : ligne
- Identifiez la zone de code de cette procédure CUDA : lignes
- Identifiez le noyau CUDA appelé par cette procédure : lignes
- Examinez dans cette procédure la construction du noyau CUDA : ligne
- Examinez dans cette procédure l'appel du noyau CUDA : ligne
- Quelles similarités distinguez-vous entre les noyaux OpenCL et CUDA ?
Exploitation du programme
Ainsi, si nous voulons étudier la scalabilité du CPU en Work items de 1 à 16x le nombre de coeurs (ici 8 physiques) en exploitant l'implémentation AMD de OpenCL, nous appelons la commande :
python3 PiXPU.py -d 0 -b 1 -e $((8*16)) -r 10 -i 1000000000
Dans notre cas, nous avons les deux fichiers suivants à exploiter :
Pi_FP32_MWC_xPU_OpenCL_1_128_1_1_1000000000_Device0_InMetro_opencluster2.npzPi_FP32_MWC_xPU_OpenCL_1_128_1_1_1000000000_Device0_InMetro_opencluster2
Nous pouvons ensuite exploiter l'outil simple gnuplot pour afficher nos résultats :
gnuplot set xlabel 'Parallel Rate' set ylabel 'Itops' set yrange [0:*] plot 'Pi_FP32_MWC_xPU_OpenCL_1_128_1_1_1000000000_Device0_InMetro_opencluster2' using 1:9 title 'OpenCL AMD'
Il existe un bouton d'export du graphique en image au format PNG ou SVG. Nous obtenons le suivant :
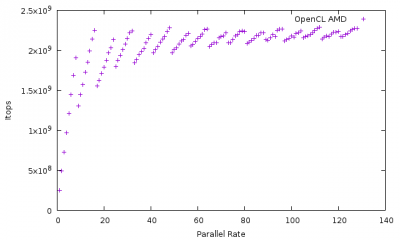
Nous observons que la scalabilité pour un code aussi simple n'est pas si triviale que cela à analyser. Il n'y a pas continuité en fonction de PR croissant. Notons une pseudo-période correspondant au nombre de coeurs physiques, avec des maximums locaux pour les multiples de cette valeur (le handsaw curve effect).
- Identifiez avec
python3 PiXPU.py -hun périphérique CPU - Exécutez le d'un PR=1 à un PR égal à 8x le nombre de coeurs physiques
- Tracez les résultats avec GNUplot
Nous pouvons également “explorer” la scalabilité des GPU forts de notre expérience de PiOpenCL. Par exemple, du nombre de cuda cores à ce nombre multiplié par 16, par pas de 128. La commande appelée est la suivante :
python3 PiXPU.py -d 2 -b 3584 -e $((3584*8)) -s 128 -r 3 -i 100000000000
Nous obtenons pour notre GTX 1080 Ti les résultats suivants :
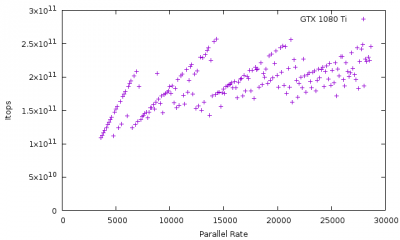
Nous pouvons constater que la scalabilité est très peu continue, encore moins que pour la scalabilité étudiée des CPU. Nous constatons également que des pseudo-lignes se chevauchent. Le PR optimal était autour de 4x le nombre de cuda cores et offrait une performance de 268 Gitops.
- Identifiez avec
python3 PiXPU.py -hun périphérique GPU - Exécutez-le d'un PR=<NbCudaCores> à un PR égal à 8x<NbCudaCores> par pas de 128 en OpenCL
- Tracez les résultats avec GNUplot
- Identifiez pour quel PR la performance est maximale
Comme nous avons également la même implémentation en CUDA, lançons l'exploration avec CUDA pour le PR optimal, ici identifié à 4x le nombre de cuda cores :
python3 PiXPU.py -g CUDA -d 0 -b $((3584*4)) -e $((3584*4)) -r 3 -i 10000000000
Comme résultat de cette implémentation CUDA, nous n'obtenons pas 268 Gitops, mais seulement 6 Gitops !
La seule manière de retrouver une performance comparable en CUDA est de solliciter le second étage de parallélisme des GPU, les Threads. Avec la commande suivante, avec 1024 Threads, nous plafonnons à 198 Gitops :
python3 PiXPU.py -g CUDA -d 0 -b $((3584*4)) -e $((3584*4)) -f 1024 -l 1024 -r 3 -i 1000000000000
En relançant le calcul précédent, nous parvenons à 271 Gitops soit plus que l'implémentation OpenCL.
- Identifiez avec
python3 PiXPU.py -hle périphérique GPU déjà utilisé en CUDA - Exécutez le avec le PR optimal des Blocks en CUDA
- Quel ratio de performance avez-vous entre CUDA et OpenCL ?
- Exécutez le avec le PR optimal des Blocks et 1024 Threads
- Quel ratio de performance avez-vous entre CUDA et OpenCL ?
Il existe aussi des artéfacts sur des régimes de parallélisme spéciaux en OpenCL sur les GPU Nvidia : en explorant autour du PR optimal, quelles sont les PR qu'il ne faut surtout pas exploiter et quel est leur point commun ?
En lançant cette exploration suivante, nous obtenons :
python3 PiXPU.py -d 2 -b $((3584*4-16)) -e $((3584*4+16)) -r 3 -i 100000000000
Alors que l'optimum de performance est atteint autour d'un PR de 14336 avec 258 Gitops, nous n'obtenons un Itops que de 8.5 Gitops (soit 30x moins) sur 5 valeurs particulières : 14321, 14323, 14327, 14341, 14347. Le point commun entre ces valeurs de PR est à rechercher sur le site de mathématiques
- Exécutez
PiXPU.pyautour du PR égal à 4x le nombre de cuda cores (16 avant et 16 après) - Tracez les résultats avec GNUplot
- Quels sont les PR avec les performances les plus faibles ?
Exploration par un corps N-Corps à "grain fin"
Le code de test Pi Monte Carlo avait pour avantage de ne solliciter que très peu la mémoire. La seule mémoire sollicitée sur les périphériques se résumait au nombre de tirages dans le quadrant de cercle. De plus, l'opération de parallélisation divisait un nombre total d'itérations en un nombre équivalent pour chaque work item, chaque block ou chaque thread. Chaque calcul était indépendant des autres : nous avions non seulement un code ALU (ne sollicitant que les unités de traitement) mais aussi un code gros grain (indépendance des calculs).
Dans le code NBody.py, situé dans bench4gpu/NBody, le principe est de déterminer dans un modèle newtonien la position et la vitesse de chaque particule en intéraction avec toutes les autres. A chaque itération, chaque position et chaque vitesse de chaque particule vont être modifiées par la proximité de toutes les autres : nous disposons d'un code grain fin. De plus, la détermination de la vitesse et la position de chaque particule à chaque instant nécessite un accès à la position de chacune des autres : un accès permanent à la mémoire est donc indispensable.
Le programme NBody.py n'est disponible qu'en OpenCL. Son invocation avec l'option -h offre la sortie suivante :
$ cd $HOME/bench4gpu/NBody $ python3 NBody.py -h NBody.py -h [Help] -r [InitialRandom] -g [OpenGL] -e [VirielStress] -o [Verbose] -p [Potential] -x <None|NegExp|CorRad> -d <DeviceId> -n <NumberOfParticules> -i <Iterations> -z <SizeOfBoxOrBall> -v <Velocity> -s <Step> -b <Ball|Box> -m <ImplicitEuler|RungeKutta|ExplicitEuler|Heun> -t <FP32|FP64> Informations about devices detected under OpenCL: Device #0 from Advanced Micro Devices, Inc. of type xPU : Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz Device #1 from The pocl project of type xPU : pthread-Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz Device #2 from NVIDIA Corporation of type xPU : GeForce GTX 1080 Ti Device #3 from NVIDIA Corporation of type xPU : Quadro K420 Device #4 from Intel(R) Corporation of type xPU : Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz
Un certain nombre des paramètres sont à définir avec une valeur :
-d <DeviceId>: sélection du périphérique (défaut 0)-n <NumberOfParticules>: nombre de particules du système (défaut 2)-s <Step>: pas d'intégration (défaut 1/32)-m <ImplicitEuler|RungeKutta|ExplicitEuler|Heun>: type d'intégration différentielle (défaut ImplicitEuler)-t <FP32|FP64>: précision de calcul (défaut FP32)-i <Iterations>: nombre d'itérations (défaut 10)-x <None|NegExp|CorRad>: introduction d'un “rayon de coeur” pour éviter les divergences (défaut None)-z <SizeOfBoxOrBall>: taille de la boîte ou de la boule (défaut sqrt(2))-v <Velocity>: vitesse initiale des particules (défaut définie par le Viriel)-b <Ball|Box>: type de distribution aléatoire (défaut Ball)
D'autres sont des booléens :
-h [Help]: la sortie précédente-r [InitialRandom]: défaut-g [OpenGL]: pour une sortie graphique-e [VirielStress]: par défaut-o [Verbose]: impression position et vitesse des particules-p [Potential]: exploitation du potentiel à la place de la force
Par défaut, une invocation sans option offre la sortie suivante :
python3 NBody.py
Device choosed : 0
Number of particules : 2
Size of Shape : 1.4142135
Initial velocity : 1.0
Step of iteration : 0.03125
Number of iterations : 10
Method of resolution : ImplicitEuler
Initial Random for RNG Seed : False
ValueType is : FP32
Viriel distribution of stress : True
OpenGL real time rendering : False
Speed rendering : False
Interaction type : Force
Counter Artevasion type : None
('CPU/GPU selected: ', 'Intel(R) Xeon(R) CPU E5-2637 v4 @ 3.50GHz')
('Platform selected: ', 'AMD Accelerated Parallel Processing')
/usr/lib/python2.7/dist-packages/pyopencl/cffi_cl.py:1470: CompilerWarning: Non-empty compiler output encountered. Set the environment variable PYOPENCL_COMPILER_OUTPUT=1 to see more.
"to see more.", CompilerWarning)
All particles superimposed.
All particules distributed
Center Of Mass estimated: (-0.05390843,0.25029457,-0.0005747825)
All particules stressed
Energy estimated: Viriel=-5.960464477539063e-08 Potential=-0.94194394 Kinetic=0.47097194
Starting!
..........
Ending!
Center Of Mass estimated: (-0.05390393,0.25027496,-0.00055484474)
Energy estimated: Viriel=-2.7835369110107422e-05 Potential=-0.94973665 Kinetic=0.4748544
Duration stats on device 0 with 10 iterations :
Mean: 0.0017527103424072265
Median: 0.00153350830078125
Stddev: 0.0007242915279449818
Min: 0.0013959407806396484
Max: 0.0039031505584716797
Variability: 0.4723101450288789
FPS stats on device 0 with 10 iterations :
Mean: 623.2326583734787
Median: 653.6473926380554
Stddev: 130.28936462458745
Min: 256.2032862989432
Max: 716.3627668659266
Squertz in log10 & complete stats on device 0 with 10 iterations :
Mean: 3.396710194304037 2492.9306334939147
Median: 3.417403524471372 2614.5895705522216
Stddev: 2.716968957513558 521.1574584983498
Min: 3.01064468743274 1024.813145195773
Max: 3.4571929965271666 2865.4510674637063
Les éléments de sortie sont les statistiques de chaque itération, exprimées en squertz, contraction de square (pour “carré”) avec Hertz. En effet, le nombre de calculs élémentaires évolue suivant une loi en N(N-1) (chaque particule parmi N intéragit avec les N-1 autres particules).
Analyse du programme
Lors de l'initialisation du “système N-Corps”, plusieurs opérations sont effectuées :
- l'initialisation de la position des particules
- la distribution aléatoire des particules dans le volume (boule ou cube)
- la détermination du centre de gravité
- la distribution semi-aléatoire des vitesses en fonction du Viriel
- l'évolution du système
NBody.py- Editez le programme avec gedit
- Identifiez le bloc de noyaux OpenCL : lignes
- Identifiez les appels des noyaux OpenCL : lignes
- Identifiez les récupérations de positions et vitesses des particules
- Identifiez la portion de code OpenGL
Pour un lancement sur 32768 particules et les différents périphériques (3 CPU et 2 GPU), pour des calculs en 32 et 64 bits en flottants, nous avons les résultats suivants :
| Périphérique | Squertz SP | Squertz DP |
|---|---|---|
| AMD | 2583647198 | 1141839568 |
| PortableCL | 1277518016 | 782950973 |
| GTX 1080 Ti | 104176444905 | 2853097176 |
| QuadroK420 | 3242286836 | 116285732 |
| Intel | 4728894103 | 1444506859 |
La figure ci-dessus illustre l'écrasante performance de la GTX 1080 Ti en comparaison de toutes les autres implémentations : plus d'un facteur 22 en simple précision et presque un facteur 2 en double précision pour la meilleure des implémentations CPU.
Seule une représentation en log permet de ne pas trop écraser les performances des implémentations CPU.
NBody.py pour 32768 particules- Exécutez le programme pour tous les périphériques détectés
- Ajoutez l'option pour un calcul en 64 bits et réexécutez
- Tracez les histogrammes de performances
- Quel est le ratio entre la meilleure GPU et la meilleure en CPU en 32 bits
- Quel est le ratio entre la meilleure GPU et la meilleure en CPU en 64 bits
- Quel est le ratio pour un même périphérique entre 32 et 64 bits ?
Vous pouvez également exécuter NBody.py avec l'option -g pour disposer d'une animation en temps réel du calcul.
La fenêtre de rendu offre la vision suivante :
La pression sur la touche <Esc> permet de sortir du programme pour afficher les statistiques de la simulation.
Si nous changeons de manière insignifiante le nombre de particules (de 8192 à 8191), nous obtenons des performances très différentes :
NBody.py en mode -g- Exécutez le programme pour la meilleure implémentation sur CPU sur 8192 particules
- Appuyez sur
spour passer des positions aux vitesses - Utilisez les flèches pour les opérations de rotations
- Utilisez les <+> ou ↔ pour les opérations de zoom ou dézoom
- Sortez avec <Esc> et notez finalement la performance médiane en Squertz
- Exécutez le programme sur la GPU la plus puissante avec 8192 particules
- Sortez avec <Esc> et notez la performance médiane en Squertz
- Exécutez le programme sur la GPU la plus puissante avec 8191 particules
- Sortez avec <Esc> et notez la performance médiane en Squertz
- Quel ratio entre Squertz existe entre 8192 et 8191 particules ?
- Pourquoi un tel ratio ?
Conclusion
Comme vous l'aurez remarqué au cours de ces Travaux Pratiques, l'exploitation peut être pleine de surprises : une métrologie pertinente ne peut se passer de la connaissance du matériel exploité.
L'exploitation de “codes métier” vous aura aussi permis d'entrevoir la difficulté d'intégrer et d'exécuter des programmes dans des environnements pourtant bien homogènes : toutes les stations exploitées ont exactement le même système d'exploitation, SIDUS. Les “astuces” permettant de simplement pouvoir exécuter les programmes illustraient aussi que, sans expérience, difficile de s'en sortir.
— Emmanuel Quemener 2022/07/20 15:13